题目内容
16.已知盒子中有六张分别标有数字1、2、3、4、5、6的卡片(Ⅰ)现从盒子中任取两张卡片,将卡片上的数字相加,求所得数字是奇数的概率;
(Ⅱ)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张标有数字为偶数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列.
分析 (Ⅰ)现从盒子中任取两张卡片,将卡片上的数字相加,所得数字是奇数,为奇数+偶数,即可求出概率;
(Ⅱ)由于抽到偶数就停止抽取,故抽取次数最多四次就停止,故变量的取值为1,2,3,4,分别计算出它们的概率,得出抽取次数ξ的分布列.
解答 解:(Ⅰ)计事件A为“任取两张卡片,卡片上的数字相加得到的数字是奇数”,
所以$P(A)=\frac{C_3^1C_3^1}{C_6^2}=\frac{3}{5}$ …(4分)
(Ⅱ)ξ可取1,2,3,4.
$P(ξ=1)=\frac{C_3^1}{C_6^1}=\frac{1}{2},P(ξ=2)=\frac{C_3^1}{C_6^1}•\frac{C_3^1}{C_5^1}=\frac{3}{10}$,$P(ξ=3)=\frac{C_3^1}{C_6^1}•\frac{C_2^1}{C_5^1}•\frac{C_3^1}{C_4^1}=\frac{3}{20},P(ξ=4)=\frac{C_3^1}{C_6^1}•\frac{C_2^1}{C_5^1}•\frac{C_1^1}{C_4^1}•\frac{C_3^1}{C_3^1}=\frac{1}{20}$; …(10分)
故ξ的分布列为
| ξ | 1 | 2 | 3 | 4 |
| P | $\frac{3}{10}$ | $\frac{3}{10}$ | $\frac{3}{20}$ | $\frac{1}{20}$ |
点评 本题考查离散型随机变量的分布列,正确理解所研究的事件,得出变量的取值范围是求分布列的第一步,解题时要考虑周全.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
5.执行如图所示的程序框图,则输出k的值为( )
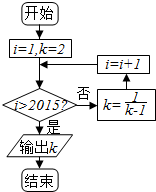

| A. | -1 | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
