题目内容
设直线x=m与函数f(x)=x2+4,g(x)=2lnx的图象分别交于点M、N,则当|MN|达到最小时m的值为( )
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
考点:利用导数研究函数的极值,二次函数的性质,对数函数的图像与性质,利用导数研究函数的单调性
专题:导数的综合应用
分析:当x=m时,|MN|=m2+4-2lnm,然后利用导数求出函数的最小值即可.
解答:
解:当x=m时,|MN|=m2+4-2lnm,m>0,
设f(m)=|MN|=m2+4-2lnm,
则f'(m)=2m-
=
,
由f'(m)>0得m>1,此时函数单调递增,
由f'(m)<0得0<m<1,此时函数单调递减,
即当m=1时,函数取得极小值,同时也是最小值为f(1)=1+4-2ln1=5.
此时m=1.
故选:C.
设f(m)=|MN|=m2+4-2lnm,
则f'(m)=2m-
| 2 |
| m |
| 2(m2-1) |
| m |
由f'(m)>0得m>1,此时函数单调递增,
由f'(m)<0得0<m<1,此时函数单调递减,
即当m=1时,函数取得极小值,同时也是最小值为f(1)=1+4-2ln1=5.
此时m=1.
故选:C.
点评:本题主要考查函数最值的求法,利用导数研究函数的极值是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,AB是⊙O的直径,弦CD交AB于点P,PA=2,PC=6,PD=4,则AB等于( )


| A、3 | B、8 | C、12 | D、14 |
已知椭圆C1:
+
=1(a1>b1>0)与双曲线C2:
-
=1(a2>0,b2>0)有相同的焦点F1,F2,点P是两曲线的一个公共点,a1,a2又分别是两曲线的离心率,若PF1⊥PF2,则4e12+e22的最小值为( )
| x2 |
| a12 |
| y2 |
| b12 |
| x2 |
| a22 |
| y2 |
| b22 |
A、
| ||
| B、4 | ||
C、
| ||
| D、9 |
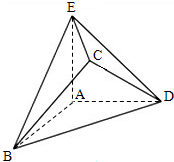 如图,在几何体ABCDE中,AB=AD=BC=DC=2,AE=2
如图,在几何体ABCDE中,AB=AD=BC=DC=2,AE=2