题目内容
19.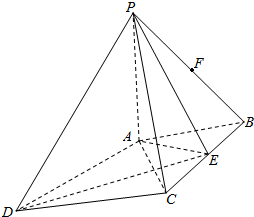 如图,PA⊥平面ABCD,四边形ABCD是菱形,AB=1,∠ABC=60°,PD与平面ABCD所成的角是45°.点E是BC的中点,点F在边PB上.
如图,PA⊥平面ABCD,四边形ABCD是菱形,AB=1,∠ABC=60°,PD与平面ABCD所成的角是45°.点E是BC的中点,点F在边PB上.(1)当F位于PB什么位置时,EF∥平面PAC;
(2)证明:平面PBC⊥平面PAE.
分析 (1)由点E是BC的中点,点F是PB中点,得EF∥PC,由此得到EF∥平面PAC.
(2)由已知得AC=AB=1,∠PDA=45°,PA=1,从而BC⊥AE,BC⊥PE,由此能证明平面PBC⊥平面PAE.
解答 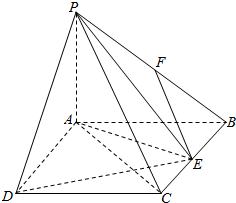 解:(1)当F是PB中点时,EF∥平面PAC.
解:(1)当F是PB中点时,EF∥平面PAC.
理由如下:
∵点E是BC的中点,点F是PB中点,
∴EF∥PC,
∵EF?平面PAC,PC?平面PAC,
∴EF∥平面PAC.
证明:(2)∵PA⊥平面ABCD,四边形ABCD是菱形,
AB=1,∠ABC=60°,PD与平面ABCD所成的角是45°,点E是BC的中点,
∴AC=AB=1,∠PDA=45°,∴PA=1,
∴BC⊥AE,PC=PB,∴BC⊥PE,
∵AE∩PE=E,∴BC⊥平面PAE,
∵BC?PBC,∴平面PBC⊥平面PAE.
点评 本题考查使线面平行的点的位置的判断与求法,考查面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设抛物线y2=16x的焦点为F,点P在此抛物线上,且横坐标为5,则|PF|等于( )
| A. | 13 | B. | 8 | C. | 9 | D. | 10 |
 是圆
是圆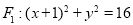 上任意一点(
上任意一点(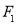 是圆心),点
是圆心),点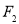 与点
与点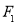 关于原点对称.线段
关于原点对称.线段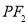 的中垂线
的中垂线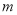 分别与
分别与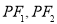 交于
交于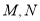 两点.
两点.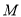 的轨迹
的轨迹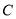 的方程;
的方程;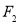 ,与抛物线
,与抛物线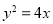 交于
交于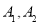 两点,与
两点,与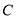 交于
交于 两点.当以
两点.当以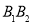 为直径的圆经过
为直径的圆经过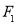 时,求
时,求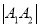 .
.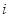 是虚数单位,
是虚数单位,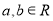 ,则“
,则“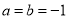 ”是“
”是“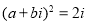 ”的( )
”的( )