题目内容
4.化简式子cos($\frac{3π}{2}$-α)•sin($\frac{9π}{2}$+α)•tan(π-α)的结果为sin2α.分析 根据诱导公式即可化简.
解答 解:cos($\frac{3π}{2}$-α)•sin($\frac{9π}{2}$+α)•tan(π-α)=-sinαcosα(-tanα)=sin2α,
故答案为:sin2α.
点评 本题主要考查了诱导公式,属于基础题.

练习册系列答案
相关题目
16.若函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-2ax-1,x≥1}\\{ax-1,x<1}\end{array}\right.$在R上是增函数,则实数a的取值范围是( )
| A. | 0$<a≤\frac{1}{3}$ | B. | 0<a≤1 | C. | a≤1 | D. | a>0 |
9.已知函数f(2x)=log3(x-2)+|1-x|,则f(6)=( )
| A. | 2 | B. | 3 | C. | 5 | D. | 8 |
4.已知三棱锥P-ABC,点P,A,B,C都在半径为2$\sqrt{3}$的球面上,若PA,PB,PC两两互相垂直且相等,则球心到截面ABC的距离为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
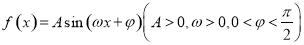 的图象经过三点
的图象经过三点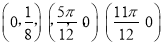 ,且在区间
,且在区间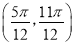 内有唯一的最值,且为最小值.
内有唯一的最值,且为最小值.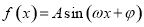 的解析式;
的解析式;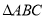 中,
中,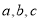 分别是角
分别是角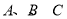 的对边,若
的对边,若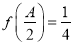 且
且 ,求
,求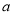 的值.
的值.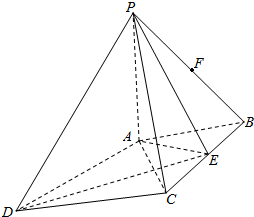 如图,PA⊥平面ABCD,四边形ABCD是菱形,AB=1,∠ABC=60°,PD与平面ABCD所成的角是45°.点E是BC的中点,点F在边PB上.
如图,PA⊥平面ABCD,四边形ABCD是菱形,AB=1,∠ABC=60°,PD与平面ABCD所成的角是45°.点E是BC的中点,点F在边PB上. ,
, ,且
,且 与
与 夹角为
夹角为 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
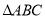 的内接正方形面积的最大值为____________.
的内接正方形面积的最大值为____________.