题目内容
15.设集合A={x|(x+2)(x-3)<0},B={x|4x+c<0}.(1)若A⊆B,求实数c的取值范围;
(2)若A∩∁RB={x|1≤x<3},求实数c的值.
分析 (1)求出集合A、B,利用A⊆B,列出不等式求解即可.
(2)求出集合B的补集,利用A∩∁RB={x|1≤x<3},求实数c的值.
解答 解:(1)集合A={x|(x+2)(x-3)<0}={x|-2<x<3},B={x|4x+c<0}={x|x$<-\frac{c}{4}$},
A⊆B,可得:$3≤-\frac{c}{4}$,解得c≤-12.
实数c的取值范围:(-∞,-12].
(2)∵B={x|x$<-\frac{c}{4}$},
∁RB={x|x$≥-\frac{c}{4}$}.
A∩∁RB={x|1≤x<3},
可得$1=-\frac{c}{4}$,
解得c=-4.
点评 本题考查集合的表示方法、子集的定义,两个集合的交集、并集的定义和求法,准确理解子集,交集,并集的定义,是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
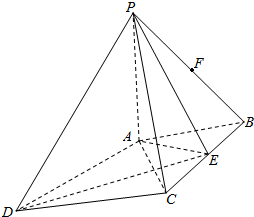 如图,PA⊥平面ABCD,四边形ABCD是菱形,AB=1,∠ABC=60°,PD与平面ABCD所成的角是45°.点E是BC的中点,点F在边PB上.
如图,PA⊥平面ABCD,四边形ABCD是菱形,AB=1,∠ABC=60°,PD与平面ABCD所成的角是45°.点E是BC的中点,点F在边PB上. ,集合
,集合 ,则
,则 为( )
为( ) B.
B. C.
C. D.
D.
 的终边经过点
的终边经过点 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.0
D.0