题目内容
2.在△ABC中,已知AB=AC=5,BC=6,则$\overrightarrow{AB}•\overrightarrow{AC}$=( )| A. | 18 | B. | 12 | C. | 7 | D. | 24 |
分析 可作出图形,并取BC的中点D,连接AD,从而可得出AD⊥BD,这样在Rt△ABD中可求出$sin∠BAD=\frac{3}{5}$,进而可求出cos∠BAC的值,从而由向量数量积的计算公式即可求出$\overrightarrow{AB}•\overrightarrow{AC}$的值.
解答 解:如图,取BC中点D,连接AD,则:AD⊥BD;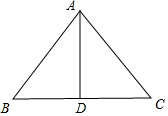 ∴$sin∠BAD=\frac{3}{5}$;
∴$sin∠BAD=\frac{3}{5}$;
∴$cos∠BAC=1-2si{n}^{2}∠BAD=1-\frac{18}{25}$=$\frac{7}{25}$;
∴$\overrightarrow{AB}•\overrightarrow{AC}=|\overrightarrow{AB}||\overrightarrow{AC}|cos∠BAC$=$5×5×\frac{7}{25}=7$.
故选C.
点评 考查等腰三角形的底边的中线也是高线,三角函数的定义,二倍角的余弦公式,以及向量数量积的计算公式.

练习册系列答案
相关题目
10.已知椭圆过点(0,3)且与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{7}$=1有相同的焦点,则椭圆的标准方程为( )
| A. | $\frac{{x}^{2}}{7}+\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{7}$=1 | C. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{7}$=1 | D. | $\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1 |
1.已知某一随机变量ξ的概率分布如下,且E(ξ)=6.3,则a的值为7.
| ξ | 4 | a | 9 |
| P | 0.5 | 0.1 | b |
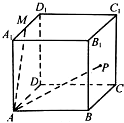 在棱长为1的正方体ABCD-A1B1C1D1中,M是A1D1的中点,点P在侧面 BCC1B1上运动.现有下列命题:
在棱长为1的正方体ABCD-A1B1C1D1中,M是A1D1的中点,点P在侧面 BCC1B1上运动.现有下列命题: