题目内容
18.直线$\sqrt{3}$x+3y-k=0与圆C:(x-2)2+(y-3)2=4相交于A、B两,当扇形ABC的面积大于等于$\frac{2π}{3}$时,k的取值区间长度为( )| A. | 4$\sqrt{3}$ | B. | 6 | C. | 2$\sqrt{3}$ | D. | 12 |
分析 利用扇形ABC的面积大于等于$\frac{2π}{3}$,求出∠ACB=α≥$\frac{π}{3}$,可得圆心到直线的距离d=$\frac{|2\sqrt{3}+9-k|}{\sqrt{3+9}}$≤$\sqrt{3}$,即可求出k的取值区间长度
解答 解:∵扇形ABC的面积大于等于$\frac{2π}{3}$,
∴$\frac{1}{2}×2×2×α$≥$\frac{2π}{3}$,
∴∠ACB=α≥$\frac{π}{3}$,
∴圆心到直线的距离d=$\frac{|2\sqrt{3}+9-k|}{\sqrt{3+9}}$≤$\sqrt{3}$,
∴3-2$\sqrt{3}$≤k≤15-2$\sqrt{3}$,
∴k的取值区间长度为12.
故选:D.
点评 本题考查扇形面积的计算,考查点到直线的距离公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
9.函数f(x)=x3-$\frac{1}{x}$的图象关于( )
| A. | y轴对称 | B. | 直线y=-x对称 | C. | 坐标原点对称 | D. | 直线y=x对称 |
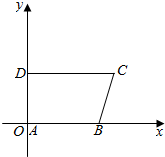 设直角梯形ABCD,DA⊥AB,在两平行边AB、DC上有两个动点P、Q,直线PQ平分梯形的面积,求证:PQ必过一个定点.
设直角梯形ABCD,DA⊥AB,在两平行边AB、DC上有两个动点P、Q,直线PQ平分梯形的面积,求证:PQ必过一个定点.