题目内容
如图，在正方体ABCD-A1B1C1D1中，M、N分别是BB1、CD中点，则异面直线A1M、C1N所成角的大小为（ ）| A、30° | B、45° |
| C、60° | D、90° |
考点：异面直线及其所成的角
专题：空间角,空间向量及应用
分析：建立空间直角坐标系，求出向量
，
的坐标，根据坐标可求这两向量的夹角，从而求出对应异面直线所成的角．
| A1M |
| C1N |
解答：
解：设该正方体的边长为1，建立如下图所示空间直角坐标系：
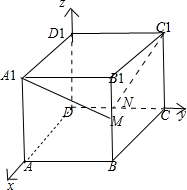能确定以下几点的坐标：
A1（1，0，1），M（1，1，
），C1（0，1，1），N（0，
，0）；
∴
=(0，1，-
)，
=(0，-
，-1)；
∴
•
=0，∴
⊥
；
∴异面直线A1M、C1N所成角的大小为90°．
故选D．
能确定以下几点的坐标：A1（1，0，1），M（1，1，
| 1 |
| 2 |
| 1 |
| 2 |
∴
| A1M |
| 1 |
| 2 |
| C1N |
| 1 |
| 2 |
∴
| A1M |
| C1N |
| A1M |
| C1N |
∴异面直线A1M、C1N所成角的大小为90°．
故选D．
点评：考查异面直线所成的角以及通过建立空间直角坐标系，用向量求解异面直线所成角的方法．
练习册系列答案
相关题目
直线l与函数f（x）=-sinx（x∈[-π，0]）的图象相切于点A，且l∥OP，其中O为坐标原点，P（xp，yp）在f（x）图象上，且f′（xp）=0，则点A的纵坐标是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={1，2，4}，B={1，x}，若B⊆A，则x=（ ）
| A、1 | B、2 |
| C、2或4 | D、1或2或4 |
在（1-x）20的展开式中，如果第4r项和第r+2项的二项式系数相等，则r的值为（ ）
| A、4 | B、5 | C、6 | D、7 |
已知向量
=（2，3），
=（-3，0），则向量
的坐标为（ ）
| AB |
| BC |
| AC |
| A、（5，3） |
| B、（-1，3） |
| C、（-5，-3） |
| D、（1，-3） |
设P为椭圆上一点，且∠PF1F2=30°∠PF2F1=45°，其中F1，F2为椭圆的两个焦点，则椭圆的离心率e的值等于（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
在半径为2的半圆圆周上取两点A、B，则圆心角∠AOB＜
的概率为（ ）
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
三名学生分别从计算机、英语两学科中选修一门课程，不同的选法有（ ）
| A、3种 | B、6种 | C、8种 | D、9种 |