题目内容
13.已知F1,F2分别为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,过F2作双曲线一条渐近线的垂线,垂足为M,且|MF1|=3|MF2|,则此双曲线的离心率是$\frac{\sqrt{6}}{2}$.分析 求出双曲线的一条渐近线方程,运用点到直线的距离公式,求得|MF2|=b,运用余弦函数的定义和余弦定理,结合离心率公式,计算即可得到所求值.
解答 解:设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线方程为y=$\frac{b}{a}$x,
F2(c,0)到渐近线的距离为d=|MF2|=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=b,
cos∠MOF2=$\frac{|MO|}{|O{F}_{2}|}$=$\frac{\sqrt{{c}^{2}-{b}^{2}}}{c}$=$\frac{a}{c}$,
在△MOF1中,|MF1|2=|MO|2+|OF1|2-2|MO|•|OF1|•cos∠MOF2
=a2+c2-2ac•(-$\frac{a}{c}$)=3a2+c2,
由|MF1|=3|MF2|,可得3a2+c2=9b2=9(c2-a2),
即有c2=$\frac{3}{2}$a2,即e=$\frac{c}{a}$=$\frac{\sqrt{6}}{2}$.
故答案为:$\frac{\sqrt{6}}{2}$.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的渐近线方程和点到直线的距离公式,同时考查余弦定理的运用,化简整理的运算能力,属于中档题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
6.若奇函数y=g(x)与f(x)=2sin(2x+φ)图象关于直线x=$\frac{π}{6}$对称,要得到y=g(x),则可用y=f(x)的图象变换得到(|φ|<$\frac{π}{2}$),需经过的变换是( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
8.已知双曲线C的焦点为F1,F2,点P是双曲线上任意一点,若双曲线的离心率为2,且|PF1|=2|PF2|,则cos∠PF2F1=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
18.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点F作一条渐近线的垂线,垂足为P,线段OP的垂直平分线交y轴于点Q(其中O为坐标原点).若△OFP的面积是△OPQ的面积的4倍,则该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
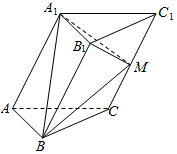 在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.
在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.