题目内容
已知双曲线C1: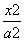 -
-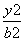 =1(a>0,b>0)与双曲线C2:
=1(a>0,b>0)与双曲线C2: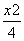 -
-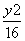 =1有相同的渐近线,且C1的右焦点为F(
=1有相同的渐近线,且C1的右焦点为F(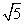 ,0),则a=________,b=________.
,0),则a=________,b=________.
1 2

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
题目内容
已知双曲线C1: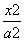 -
-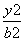 =1(a>0,b>0)与双曲线C2:
=1(a>0,b>0)与双曲线C2: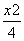 -
-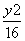 =1有相同的渐近线,且C1的右焦点为F(
=1有相同的渐近线,且C1的右焦点为F(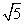 ,0),则a=________,b=________.
,0),则a=________,b=________.
1 2

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案