题目内容
1.若不等式3x2+1≥mx(x-1)对于?x∈R恒成立,则实数m的取值范围是-6≤m≤2.分析 把不等式化为(3-m)x2+mx+1≥0,利用判别式列出不等式组,求出m的取值范围.
解答 解:不等式3x2+1≥mx(x-1)可化为(3-m)x2+mx+1≥0,
该不等式对?x∈R恒成立,
当3-m=0时,不等式化为3x+1≥0,不满足条件;
∴$\left\{\begin{array}{l}{3-m>0}\\{△≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m<3}\\{{m}^{2}-4(3-m)≤0}\end{array}\right.$,
解得-6≤m≤2.
故答案为:-6≤m≤2.
点评 本题主要考查了二次函数的性质以及不等式的恒成立问题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,点A(c,b),右焦点F(c,0),椭圆上存在一点M,使得$\overrightarrow{OM}•\overrightarrow{OA}=\overrightarrow{OF}•\overrightarrow{OA}$,且$\overrightarrow{OM}+\overrightarrow{OF}=t\overrightarrow{OA}({t∈R})$,则该椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
13.已知函数f(x)的定义域是R,f(0)=2,对任意x∈R,f′(x)>f(x)+1,则下列正确的为( )
| A. | (f(1)+1)•e>f(2)+1 | B. | 3e<f(2)+1 | ||
| C. | 3•e≥f(1)+1 | D. | 3e2与f(2)+1大小不确定 |




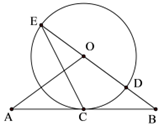 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.