题目内容
4.已知定义域为R的函数f(x)满足f(-x)=-f(x+4),且当x>2时,f(x)单调递增.如果x1+x2<4,且(x1-2)(x2-2)<0,则f(x1)+f(x2)的取值范围是( )| A. | (-∞,0) | B. | (-∞,0] | C. | (0,1] | D. | (0,+∞) |
分析 根据抽象函数关系,结合函数对称性的性质进行判断即可.
解答 解:∵(x1-2)(x2-2)<0,不妨考虑x1<2,x2>2,
则4-x1>0,
又,∵x1+x2<4,∴x2<4-x1,
∴f(x2)<f(4-x1)=-f(x1),
∴f(x1)+f(x2)<0.
同理当x2<2,x1>2,也推得同样结果.
综上f(x1)+f(x2)<0.
故选:A.
点评 本题主要考查函数单调性的应用,根据抽象函数的关系,进行转化是解决本题的关键.

练习册系列答案
相关题目
18.(-$\sqrt{x}$+$\frac{1}{x}$)10的展开式中x2的系数等于( )
| A. | 45 | B. | 20 | C. | -30 | D. | -90 |
16.如图是函数f(x)=x3+bx2+cx+d的大致图象,则b的取值范围是( )
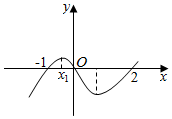

| A. | (-∞,-2) | B. | (-∞,-1) | C. | (-3,1) | D. | (1,+∞) |
13.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+4(-1≤x<0)}\\{sinπx,(x>0)}\end{array}\right.$,且f(x)-ax>-1对于定义域内的任意的x恒成立,则a的取值范围是( )
| A. | [-6,0) | B. | [-6,0] | C. | (-1,0] | D. | [-1,0] |
14.以下有关命题的说法错误的是( )
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | 若p∧q为假命题,则p,q均为假命题 | |
| C. | “a<b”是“a+c<b+c”的充要条件 | |
| D. | 命题$p:?{x_0}∈R,{e^{x_0}}≤0$为假命题 |
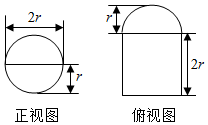 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图 中的正视图和俯视图如图所示,若 该几何体的表面积为64+80π,则 r=( )
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图 中的正视图和俯视图如图所示,若 该几何体的表面积为64+80π,则 r=( )