题目内容
6.在等差数列{an}中,a1+a5=8,a4=7.(1)求数列的第10项.
(2)问112是数列{an}的第几项?
(3)数列{an}从第几项开始大于30?
(4)在80到110之间有多少项?
分析 求出数列的通项公式,利用通项公式列出方程或不等式解出.
解答 解:(1)∵a1+a5=2a3=8,∴a3=4,∴d=a4-a3=3.
∴a10=a4+6d=7+18=25.
(2)a1=a4-3d=7-9=-2,∴an=-2+3(n-1)=3n-5.
令an=3n-5=112,解得n=39.
∴112是{an}的第39项.
(3)令an=3n-5>30,解得n>$\frac{35}{3}$.
∴数列{an}从第12项开始大于30.
(4)令80<an<110,得80<3n-5<110,解得$\frac{85}{3}<n<\frac{115}{3}$,
∵n∈N,∴29≤n≤38.
∴在80到110之间有10项.
点评 本题考查了等差数列的通项公式,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
16.设各项均为正数的数列{an}的前n项和为Sn,且满足2an+1=an+an+2,n∈N,a4a8=32,则S11的最小值( )
| A. | 22$\sqrt{2}$ | B. | 44$\sqrt{2}$ | C. | 22 | D. | 44 |
1.在等差数列{an}中,若a6+a15=10,则前20项的和S20=( )
| A. | 90 | B. | 100 | C. | 110 | D. | 120 |
18.(-$\sqrt{x}$+$\frac{1}{x}$)10的展开式中x2的系数等于( )
| A. | 45 | B. | 20 | C. | -30 | D. | -90 |
13.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+4(-1≤x<0)}\\{sinπx,(x>0)}\end{array}\right.$,且f(x)-ax>-1对于定义域内的任意的x恒成立,则a的取值范围是( )
| A. | [-6,0) | B. | [-6,0] | C. | (-1,0] | D. | [-1,0] |
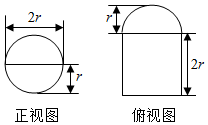 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图 中的正视图和俯视图如图所示,若 该几何体的表面积为64+80π,则 r=( )
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图 中的正视图和俯视图如图所示,若 该几何体的表面积为64+80π,则 r=( )