��Ŀ����
17������y=f��x���Ķ�����D={x|x��R����x��0}���Զ�����D����������ʵ��x1��x2������f��x1��+f��x2��=f��x1x2����������1����f��-1����ֵ��֤��y=f��x��Ϊż������
��2����f��-4��=4���� an=��-1��n•f��2n����n��N��n��1����������{an}��ǰ2015��ĺ�S2015��
��3�������� ��x��1ʱ��f��x����0���Ҳ���ʽ$f��\sqrt{{x^2}+{y^2}}����f��\sqrt{xy}��+f��a��$��������ʵ��x��y������������ʵ��a��ȡֵ��Χ��
���ģ���x��1ʱ��f��x����0�������x�IJ���ʽ f��x-3����0��
���� ��1�����ø�ֵ����f��-1����ֵ������ż�����Ķ����жϺ���Ϊż������
��2���ȸ���f��n��������{an}��ͨ�������������{an}��ǰ2015��ĺ�S2015��
��3����˵��f��x����0����0��x��1�������û�������ʽ������ɣ����ģ����ݺ���Ϊż������f��x-3����0������0��|x-3|��1���Ӷ��ɽⲻ��ʽ��
��� �⣺��1����ֵ��f��1��=f��-1��=0��
��f��-x��=f��-1��+f��x��=f��x��
�ຯ��Ϊż������
��2��f��-4��=4��f��2��=2��f��2n��=f��2n-1��+f��2����
��f��2n��=2n��
��an=2•��-1��nn��
��S2015=-2016��
��3���� $0��x��1����\frac{1}{x}��1$��
$0=f��1��=f��x��+f��\frac{1}{x}��$��
��f��x����0��0��x��1����
������$f��\sqrt{{x^2}+{y^2}}����f��\sqrt{xy}��+f��a��$��
�ã�$f��\frac{{\sqrt{{x^2}+{y^2}}}}{{a\sqrt{xy}}}����0$?$\frac{{\sqrt{{x^2}+{y^2}}}}{{|a|\sqrt{xy}}}��1$$|a|��\frac{{\sqrt{{x^2}+{y^2}}}}{{\sqrt{xy}}}$�������
��$\frac{{\sqrt{{x^2}+{y^2}}}}{{\sqrt{xy}}}��\sqrt{2}$���Ӷ�$0��|a|��\sqrt{2}$��
���ģ�f��x-3����0?0��|x-3|��1?2��x��3��3��x��4��
���� ����Ŀ����Ǻ�����������⣬��Ҫ������ʵ���ʽ�����������뺯���Ĺ�ϵ�������������⣬�ؼ��Ƿ��������������ֵ����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | f��cosA����f��cosB�� | B�� | f��sinA����f��sinB�� | C�� | f��sinA����f��cosB�� | D�� | f��sinA����f��cosB�� |
| A�� | 2 | B�� | -1 | C�� | 1 | D�� | $\frac{1}{2}$ |
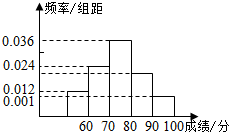 ��ij���ȫ��ѧ��һ����ѧ���Գɼ����з��������ݵķ������Ϊ��[50��60��[60��70��[70��80��[80��90��[90��100����Ƶ�ʷֲ�ֱ��ͼ��ͼ��
��ij���ȫ��ѧ��һ����ѧ���Գɼ����з��������ݵķ������Ϊ��[50��60��[60��70��[70��80��[80��90��[90��100����Ƶ�ʷֲ�ֱ��ͼ��ͼ��