题目内容
4.已知函数y=f(x)的定义R在上的奇函数,当x<0时f(x)=x+1,那么不等式f(x)<$\frac{1}{2}$的解集是( )| A. | $[{0,\frac{3}{2}})$ | B. | $({-∞,-\frac{1}{2}})∪[{0,\frac{3}{2}})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-∞,-\frac{1}{2}})∪({0,\frac{3}{2}})$ |
分析 可设x>0,从而有-x<0,根据f(x)为奇函数及x<0时f(x)=x+1便可得出x>0时,f(x)=x-1,这样便可得出f(x)在(-∞,0),[0,+∞)上为增函数,并且$f(-\frac{1}{2})=f(\frac{3}{2})=\frac{1}{2}$,讨论x:x<0时,原不等式可变成$f(x)<f(-\frac{1}{2})$,从而有$x<-\frac{1}{2}$,同理可以求出x≥0时,原不等式的解,求并集即可得出原不等式的解集.
解答 解:设x>0,-x<0,则:f(-x)=-x+1=-f(x);
∴f(x)=x-1;
∴$f(x)=\left\{\begin{array}{l}{x+1}&{x<0}\\{x-1}&{x≥0}\end{array}\right.$;
∴$f(-\frac{1}{2})=f(\frac{3}{2})=\frac{1}{2}$,且f(x)在(-∞,0),[0,+∞)上为增函数;
∴①若x<0,由$f(x)<\frac{1}{2}$得,f(x)$<f(-\frac{1}{2})$;
∴$x<-\frac{1}{2}$;
②若x≥0,由f(x)$<\frac{1}{2}$得,$f(x)<f(\frac{3}{2})$;
∴$0≤x<\frac{3}{2}$;
综上得,原不等式的解集为$(-∞,-\frac{1}{2})∪[0,\frac{3}{2})$.
故选:B.
点评 考查奇函数的定义,对于奇函数,已知一区间上的解析式,求对称区间上的解析式的方法和过程,一次函数的单调性,分段函数单调性的判断,以及根据函数单调性解不等式的方法.

练习册系列答案
相关题目
12.在一块顶角为120°、腰长为2的等腰三角形钢板废料OAB中裁剪扇形,现有如图所示两种方案,则( )
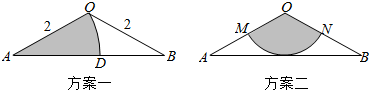

| A. | 方案一中扇形的周长更长 | B. | 方案二中扇形的周长更长 | ||
| C. | 方案一中扇形的面积更大 | D. | 方案二中扇形的面积更大 |
19.若幂函数y=f(x)的图象过点$({\frac{1}{9},\frac{1}{3}})$,则f(16)的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{4}$ | D. | 4 |
16.在下列各图中,两个变量具有较强正相关关系的散点图是( )
| A. |  | B. |  | C. |  | D. |  |
13.点M,N分别是正方体ABCD-A1B1C1D1的棱BB1和B1C1的中点,则异面直线CM与DN所成的角的余弦值为( )
| A. | $\frac{{4\sqrt{5}}}{15}$ | B. | $\frac{{\sqrt{5}}}{15}$ | C. | $\frac{{\sqrt{3}}}{15}$ | D. | $\frac{4}{15}$ |