题目内容
13.点M,N分别是正方体ABCD-A1B1C1D1的棱BB1和B1C1的中点,则异面直线CM与DN所成的角的余弦值为( )| A. | $\frac{{4\sqrt{5}}}{15}$ | B. | $\frac{{\sqrt{5}}}{15}$ | C. | $\frac{{\sqrt{3}}}{15}$ | D. | $\frac{4}{15}$ |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线CM与DN所成的角的余弦值.
解答  解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1的棱长为2,
则N(1,2,2),D(0,0,0),C(0,2,0),M(2,2,1),
则$\overrightarrow{CM}$=(2,0,1),$\overrightarrow{DN}$=(1,2,2),
设异面直线所成角为θ,
则cosθ=$\frac{|\overrightarrow{CM}•\overrightarrow{DN}|}{|\overrightarrow{CM}|•|\overrightarrow{DN}|}$=$\frac{4}{\sqrt{5}•\sqrt{9}}$=$\frac{4\sqrt{5}}{15}$.
∴异面直线CM与DN所成的角的余弦值为$\frac{4\sqrt{5}}{15}$.
故选:A.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
4.已知函数y=f(x)的定义R在上的奇函数,当x<0时f(x)=x+1,那么不等式f(x)<$\frac{1}{2}$的解集是( )
| A. | $[{0,\frac{3}{2}})$ | B. | $({-∞,-\frac{1}{2}})∪[{0,\frac{3}{2}})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-∞,-\frac{1}{2}})∪({0,\frac{3}{2}})$ |
8.2015年12月10日开始,武汉淹没在白色雾霾中,PM2.5浓度在200微克~300微克/立方米的范围,空气质量维持重度污染.某兴趣小组欲研究武昌区PM2.5浓度大小与患鼻炎人数多少之前的关系,他们分别到气象局与该地区某医院抄录了12月10日至15日的武昌区PM2.5浓度大小与该地区因患鼻炎而就诊的人数,整理得到如下资料:
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行实验.
(Ⅰ)若选取的是10号与15号的两组数据,请根据11至14号的数据,求出y关于x的线性回归方程;附:对于一组数据(x1,y1),(x2,y2),…(xn,yn),其回归直线$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x的斜率和截距的最小二乘估计分别为:$\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}({y}_{i}-\overline{y})({x}_{i}-\overline{x})}{\sum_{i=1}^{n}{({x}_{i}-\overline{x})}^{2}},\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}$
(Ⅱ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性方程是理想的,该问该小组所得线性回归方程是否理想?
| 日期 | 12月10日 | 12月11日 | 12月12日 | 12月13日 | 12月14日 | 12月15日 |
| PM2.5浓度 超过200的部分为x (微克/立方米) | 10 | 11 | 13 | 12 | 8 | 5 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
(Ⅰ)若选取的是10号与15号的两组数据,请根据11至14号的数据,求出y关于x的线性回归方程;附:对于一组数据(x1,y1),(x2,y2),…(xn,yn),其回归直线$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x的斜率和截距的最小二乘估计分别为:$\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}({y}_{i}-\overline{y})({x}_{i}-\overline{x})}{\sum_{i=1}^{n}{({x}_{i}-\overline{x})}^{2}},\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}$
(Ⅱ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性方程是理想的,该问该小组所得线性回归方程是否理想?
2.若实数数列:1,a,81成等比数列,则圆锥曲线x2+$\frac{y^2}{a}$=1的离心率是( )
| A. | $\sqrt{10}$ 或$\frac{{2\sqrt{2}}}{3}$ | B. | $\sqrt{3}$或$\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$或10 |
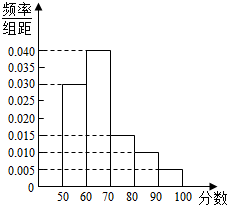 某次考试后,抽取了40位学生的成绩,并根据抽样数据制作的频率分布直方图如图所示,从成绩为[80,100]的学生中随机抽取了2人进行某项调查,则这两人分别来自两个不同分数段内的频率为$\frac{8}{15}$.
某次考试后,抽取了40位学生的成绩,并根据抽样数据制作的频率分布直方图如图所示,从成绩为[80,100]的学生中随机抽取了2人进行某项调查,则这两人分别来自两个不同分数段内的频率为$\frac{8}{15}$.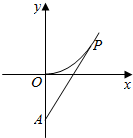 中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.
中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.