题目内容
4.在直角坐标系xOy,直线l的参数方程为$\left\{\begin{array}{l}{x=-1+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$(t为参数),以坐标原点为极点,x轴非负半轴为极轴建立极坐标系,圆C的极坐标方程式ρ=-4cosθ,则圆C的圆心到直线l的距离为$\frac{1}{2}$.分析 直线l的参数方程化为普通方程,圆的极坐标方程化为直角坐标方程,利用点到直线的距离公式,即可得出结论.
解答 解:直线l的参数方程为$\left\{\begin{array}{l}{x=-1+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$(t为参数),普通方程为x-$\sqrt{3}$y+1=0,
圆ρ=-4cosθ 即ρ2=-4ρcosθ,即 x2+y2+4x=0,即 (x+2)2+y2=4,
表示以(-2,0)为圆心,半径等于2的圆.
∴圆C的圆心到直线l的距离为$\frac{|-2+1|}{\sqrt{1+3}}$=$\frac{1}{2}$,
故答案为$\frac{1}{2}$.
点评 本题考查三种方程的转化,考查点到直线距离公式的运用,属于中档题.

练习册系列答案
相关题目
15.已知函数f(x)=f'(1)x2+x+1,则$\int_0^1{f(x)}dx$=( )
| A. | $-\frac{7}{6}$ | B. | $\frac{7}{6}$ | C. | $\frac{5}{6}$ | D. | $-\frac{5}{6}$ |
19.已知A、B分别为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右顶点,P为双曲线上一点,且△ABP为等腰三角形,若双曲线的离心率为$\sqrt{2}$,则∠ABP的度数为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 30°或120° |
14.设F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的两个焦点,若点P在双曲线上,且∠F1PF2=90°,|PF1|•|PF2|=2,则b=( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
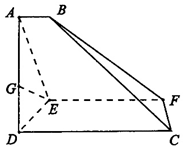 如图,已知梯形CDEF与△ADE所在的平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9,CD=12,连接BC,BF.
如图,已知梯形CDEF与△ADE所在的平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9,CD=12,连接BC,BF.