题目内容
1.函数f(x)=sin(2x+$\frac{π}{3}$)的周期T为π,函数f(x)=|sin(2x+$\frac{π}{3}$)|的周期T为$\frac{π}{2}$,f(x)=tan(-2πx+$\frac{π}{3}$)的周期为$\frac{1}{2}$,f(x)=|tan(-2πx+$\frac{π}{3}$)的周期为$\frac{1}{2}$.分析 根据正弦函数与正切函数的图象与性质,结合绝对值函数的意义,即可得出所求函数的周期T.
解答 解:函数f(x)=sin(2x+$\frac{π}{3}$)的周期T为$\frac{2π}{2}$=π,
函数f(x)=|sin(2x+$\frac{π}{3}$)|的周期T为$\frac{1}{2}$×$\frac{2π}{2}$=$\frac{π}{2}$,
f(x)=tan(-2πx+$\frac{π}{3}$)的周期为$\frac{π}{|-2π|}$=$\frac{1}{2}$,
f(x)=|tan(-2πx+$\frac{π}{3}$)|的周期为$\frac{π}{|-2π|}$=$\frac{1}{2}$.
故答案为:π,$\frac{π}{2}$,$\frac{1}{2}$,$\frac{1}{2}$.
点评 本题考查了三角函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
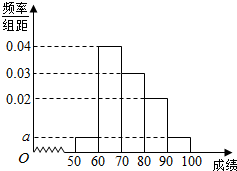 某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].