题目内容
已知等差数列 满足:
满足: ,且
,且 、
、 、
、 成等比数列.
成等比数列.
(1)求数列 的通项公式.
的通项公式.
(2)记 为数列
为数列 的前
的前 项和,是否存在正整数
项和,是否存在正整数 ,使得
,使得 若存在,求
若存在,求 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
(1)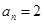 或
或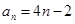 .
.
解析试题分析:(1)设数列 的公差为
的公差为 ,根据
,根据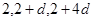 成等比数列求得
成等比数列求得 的值,从而求得数列
的值,从而求得数列 的通项公式;(2)由(1)中求得的
的通项公式;(2)由(1)中求得的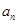 ,根据等差数列的求和公式求出
,根据等差数列的求和公式求出 ,解不等式
,解不等式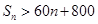 求出满足条件的的
求出满足条件的的 .
.
(1)设数列 的公差为
的公差为 ,依题意,
,依题意,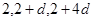 成等比数列,
成等比数列,
所以 ,解得
,解得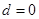 或
或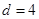 ,
,
当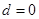 时,
时,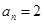 ;当
;当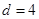 时,
时,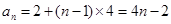 ,
,
所以数列 的通项公式为
的通项公式为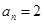 或
或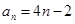 .
.
(2)当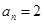 时,
时,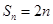 ,显然
,显然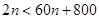 ,不存在正整数
,不存在正整数 ,使得
,使得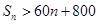 .
.
当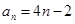 时,
时,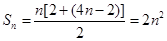 ,
,
令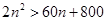 ,即
,即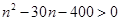 ,
,
解得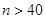 或
或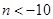 (舍去)
(舍去)
此时存在正整数 ,使得
,使得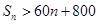 成立,
成立, 的最小值为41.
的最小值为41.
综上所述,当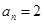 时,不存在正整数
时,不存在正整数 ;
;
当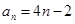 时,存在正整数
时,存在正整数 ,使得
,使得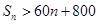 成立,
成立, 的最小值为41.
的最小值为41.
考点:等差数列、等比数列的性质,等差数列的求和公式.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
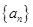 的通项公式为
的通项公式为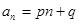 ,其中
,其中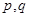 是常数,且
是常数,且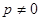 .
.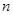 项和为
项和为 ,且
,且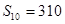 ,
,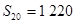 ,试确定
,试确定 的公式.
的公式.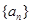 的公差为
的公差为 ,点
,点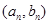 在函数
在函数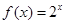 的图象上(
的图象上( ).
).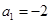 ,点
,点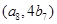 在函数
在函数 的图象上,求数列
的图象上,求数列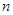 项和
项和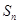 ;
;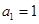 ,学科网函数
,学科网函数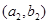 处的切线在
处的切线在 轴上的截距为
轴上的截距为 ,求数列
,求数列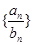 的前
的前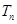 .
.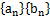 (
(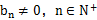 ),满足
),满足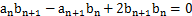 .
.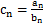 ,求数列
,求数列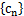 的通项公式;
的通项公式;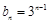 ,求数列
,求数列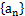 的前n项和
的前n项和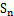
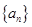 满足
满足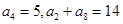 ,数列
,数列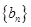 满足
满足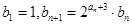 。
。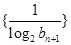 的前
的前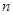 项和;
项和;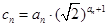 ,求数列
,求数列 的前
的前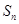
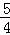 }是等比数列.
}是等比数列.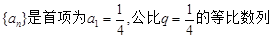 ,设数列
,设数列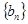 满足
满足 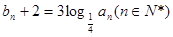 .
.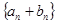 的前
的前 项和为
项和为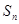 ;
; ,若
,若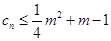 对一切正整数
对一切正整数 的取值范围.
的取值范围.