题目内容
对于抛物线y2=4x上任意一点Q，点P（a，0）都满足|PQ|≥|a|，则a的取值范围是（ ）A．（-∞，0）
B．（-∞，2]
C．[0，2]
D．（0，2）
【答案】分析：设点Q的坐标为（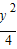
，y），根据两点之间的距离公式和|PQ|≥|a|可得y2+（
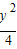-a）2≥a2，整理得a≤2+
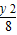，进而根据y的范围求得a的范围．
解答：解：设点Q的坐标为（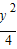
，y），
由|PQ|≥|a|，得y2+（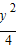
-a）2≥a2．
整理，得：y2（y2+16-8a）≥0，
∵y2≥0，∴y2+16-8a≥0，
即a≤2+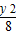
恒成立，而2+
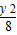的最小值为2，
∴a≤2．
故选B．
点评：本题主要考查了抛物线的性质．属基础题．
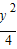，y），根据两点之间的距离公式和|PQ|≥|a|可得y2+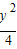（-a）2≥a2，整理得a≤2+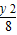，进而根据y的范围求得a的范围．解答：解：设点Q的坐标为（
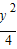，y），由|PQ|≥|a|，得y2+（
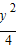-a）2≥a2．整理，得：y2（y2+16-8a）≥0，
∵y2≥0，∴y2+16-8a≥0，
即a≤2+
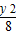恒成立，而2+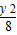的最小值为2，∴a≤2．
故选B．
点评：本题主要考查了抛物线的性质．属基础题．
练习册系列答案
相关题目
对于抛物线y2=4x上任意一点Q，点P（a，0）都满足|PQ|≥|a|，则a的取值范围是（ ）
| A、（-∞，0） | B、（-∞，2] | C、[0，2] | D、（0，2） |
