题目内容
2.如果二面角α-l-β内部一点P到α,β,l的距离分别为1,1,$\sqrt{2}$,该二面角的大小为90°.分析 由二面角α-l-β内部一点P到α,β的距离分别PA=PB=1,P到棱l的距离PO=$\sqrt{2}$,利用三垂线定理得∠AOB是二面角α-l-β的平面角,由此能求出二面角α-l-β的大小.
解答 解: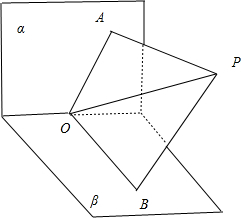 如图,二面角α-l-β内部一点P到α,β的距离分别PA=PB=1,
如图,二面角α-l-β内部一点P到α,β的距离分别PA=PB=1,
P到棱l的距离PO=$\sqrt{2}$,
则PA⊥α,A是垂足,PB⊥β,B是垂足,PO⊥l,O是垂足,
连结AO,BO,由三垂线定理得AO⊥l,BO⊥l,
∴∠AOB是二面角α-l-β的平面角,
∵AO,BO,PO都于直线l垂直,∴A、O、B、P共面,
∵PA=PB=1,PO=$\sqrt{2}$,PA⊥AO,PB⊥BO,
∴AO=BO=$\sqrt{2-1}$=1,
∴∠POA=∠POB=45°,
∴∠AOB=∠POA+∠POB=45°+45°=90°.
∴二面角α-l-β的大小为90°.
故答案为:90°.
点评 本题考查二面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
6.已知点P是△ABC所在平面内一点,且$\overrightarrow{PA}$=-2$\overrightarrow{PB}$,在△ABC内任取一点Q,则Q落在△APC内的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
7.已知i是虚数单位,若$\frac{3i}{z}$=-1+2i,则z的共轭复数$\overline{z}$等于( )
| A. | $\frac{2}{3}$+$\frac{1}{3}$i | B. | $\frac{2}{3}$-$\frac{1}{3}$i | C. | $\frac{6}{5}$+$\frac{3}{5}$i | D. | $\frac{6}{5}$-$\frac{3}{5}$i |
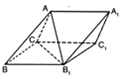 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.