题目内容
已知 为函数
为函数 图象上一点,
图象上一点, 为坐标原点。记直线
为坐标原点。记直线 的斜率
的斜率 .
.
(1)同学甲发现:点 从左向右运动时,
从左向右运动时, 不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的判断;
不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的判断;
(2)求证:当 时,
时, ;
;
(3)同学乙发现:总存在正实数 、
、 ,使
,使 .试问:他的判断是否正确?
.试问:他的判断是否正确?
(1)同学甲的判断不正确
依题意, =
= ,
, ,
,
当 时,
时, >0;当
>0;当 时,
时, <0
<0
所以, 在
在 上递增,在
上递增,在 上递减
上递减
(2)(法一) ,记
,记 ,
,
 ,
,
所以 在(1,+
在(1,+ )上为减函数,则
)上为减函数,则
 ,
,
所以 ,即
,即
(法二)要证 <
< ,即要证
,即要证 (*)
(*)
记 =
= ,有
,有 ,且
,且 ,
,
记 ,有
,有
当 时,
时, ,
, 在(1,+
在(1,+ )上递减,则
)上递减,则 <
< ,
,
所以 <0,则
<0,则 在(1,+
在(1,+ )上递减,有
)上递减,有 <
< =0
=0
即(*)式得证
(3)同学乙的判断正确


 ,且
,且 ,又由(2)
,又由(2)

 当
当 时,
时,
 ,则
,则 的图象如右图所示
的图象如右图所示
所以总存在正实数 且
且 ,使得
,使得 即
即
 ,也即为
,也即为 ,此时
,此时

练习册系列答案
相关题目
 ,给f(x)一个定义,使f(x)在点x=0处连续,则f(0)的值为
,给f(x)一个定义,使f(x)在点x=0处连续,则f(0)的值为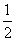
 为椭圆
为椭圆 的两个焦点,过
的两个焦点,过 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若 ,则
,则 =____________.
=____________. ,且
,且 ,
, 。则
。则 的取值范围为_______
的取值范围为_______ 的长度为
的长度为 .已知函数
.已知函数 的定义域为
的定义域为 ,值域为
,值域为 ,则区间
,则区间 绕原点逆时针旋转
绕原点逆时针旋转 ,再向右平移1个单位,所得到的直线为
,再向右平移1个单位,所得到的直线为  的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________ )
)