题目内容
下列函数中,既是奇函数又是增函数的为( )
| A、y=cosx-1 | ||
| B、y=-x2 | ||
| C、y=x•|x| | ||
D、y=-
|
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:运用常见函数的奇偶性和单调性以及定义,即可得到既是奇函数又是增函数的函数.
解答:
解:对于A.定义域为R,f(-x)=cos(-x)-1=cosx-1=f(x),则为偶函数,则A不满足条件;
对于B.定义域为R,f(-x)=f(x),则为偶函数,则B不满足条件;
对于C.定义域为R,f(-x)=(-x)|-x|=-x|x|=-f(x),则为奇函数,当x>0时,f(x)=x2递增,
且f(0)=0,当x<0时,f(x)=-x2递增,则f(x)在R上递增,则C满足条件;
对于D.定义域为{x|x≠0},关于原点对称,f(-x)=
=-f(x),当x>0时,f(x)递增,
当x<0时,f(x)递增,但在定义域内不为递增,则D不满足条件.
故选:C.
对于B.定义域为R,f(-x)=f(x),则为偶函数,则B不满足条件;
对于C.定义域为R,f(-x)=(-x)|-x|=-x|x|=-f(x),则为奇函数,当x>0时,f(x)=x2递增,
且f(0)=0,当x<0时,f(x)=-x2递增,则f(x)在R上递增,则C满足条件;
对于D.定义域为{x|x≠0},关于原点对称,f(-x)=
| 1 |
| x |
当x<0时,f(x)递增,但在定义域内不为递增,则D不满足条件.
故选:C.
点评:本题考查函数的奇偶性和单调性的判断,考查常见函数的奇偶性和单调性和定义的运用,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
下列角中,终边与310°相同的角是( )
| A、-630° | B、-50° |
| C、50° | D、630° |
复数z=
的共轭复数是( )
| -3+i |
| 2+i |
| A、-1-i | B、2-i |
| C、-1+i | D、2+i |
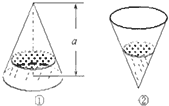 如图①,一个圆锥形容器的高为a=2,内装有高度为h的一定量的水,如果将容器倒置,这时水所形成的圆锥的高恰为1(如图②),则图①中的水面高度h=
如图①,一个圆锥形容器的高为a=2,内装有高度为h的一定量的水,如果将容器倒置,这时水所形成的圆锥的高恰为1(如图②),则图①中的水面高度h=