题目内容
19.已知a>0,函数f(x)=ax2+bx+c,若x0满足2ax0+b=0,则下列选项中是假命题的是( )| A. | ?x∈R,f(x)≤f(x0) | B. | ?x∈R,f(x)≥f(x0) | C. | ?x∈R,f(x)≤f(x0) | D. | ?x∈R,f(x)≥f(x0) |
分析 由抛物线的性质可得开口向上,x0=-$\frac{b}{2a}$为抛物线的对称轴,逐个选项验证可得.
解答 解:∵a>0,∴f(x)=ax2+bx+c所对应的抛物线开口向上,
又∵x0满足关于x的方程2ax+b=0,∴x0=-$\frac{b}{2a}$为抛物线的对称轴,
∴f(x0)为二次函数f(x)的最小值,
A、?x∈R,f(x)≤f(x0)正确;
B、?x∈R,f(x)≥f(x0) 正确;
C、?x∈R,f(x)≤f(x0)错误;
D、?x∈R,f(x)≥f(x0)正确.
故选:C.
点评 本题考查命题真假的判断,涉及二次函数的性质和特称命题以及全称命题,属基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
10.设a>0,b>0,若log4($\frac{1}{a}$+$\frac{1}{b}$)=log2$\sqrt{\frac{1}{ab}}$,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )
| A. | 8 | B. | 4 | C. | 1 | D. | $\frac{1}{4}$ |
14.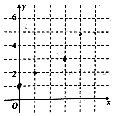 已知实数x、y的取值如表所示
已知实数x、y的取值如表所示
(1)请根据表数据在下面网格纸中绘制散点图;
(2)请根据表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
 已知实数x、y的取值如表所示
已知实数x、y的取值如表所示| x | 0 | 1 | 3 | 4 |
| y | 1 | 2 | 3 | 4.4 |
(2)请根据表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
8.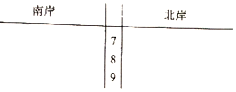 为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,经木兰溪流经河段分成10段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如表:
为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,经木兰溪流经河段分成10段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如表:
(1)记评分在80以上(包括80)为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
(2)根据表中的数据完成茎叶图:
(3)分别估计两岸分值的中位数,并计算它们的平均数,试从计算结果分析两岸环保情况,哪边保护更好?
 为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,经木兰溪流经河段分成10段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如表:
为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,经木兰溪流经河段分成10段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如表:| 南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
| 北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
(2)根据表中的数据完成茎叶图:
(3)分别估计两岸分值的中位数,并计算它们的平均数,试从计算结果分析两岸环保情况,哪边保护更好?
9.下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
| A. | f(x)=x3 | B. | f(x)=x${\;}^{\frac{1}{2}}$ | C. | f(x)=3x | D. | f(x)=($\frac{1}{2}$)x |
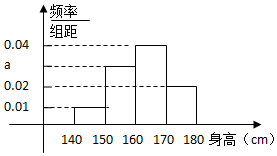 某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如图(单位:cm)