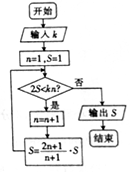
题目内容
14.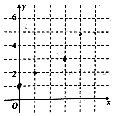 已知实数x、y的取值如表所示
已知实数x、y的取值如表所示| x | 0 | 1 | 3 | 4 |
| y | 1 | 2 | 3 | 4.4 |
(2)请根据表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
分析 (1)根据表数据绘制出散点图即可;
(2)根据表中数据,计算平均数与回归系数,写出回归直线方程即可.
解答 解:(1)根据表数据在网格纸中绘制散点图,如下;
(2)根据表中数据,得;
$\overline{x}$=$\frac{1}{4}$×(0+1+3+4)=2,
$\overline{y}$=$\frac{1}{4}$×(1+2+3+4.4)=2.6,
∴回归系数为
$\widehat{b}$=$\frac{{{\sum_{i=1}^{4}x}_{i}y}_{i}-4\overline{x}\overline{y}}{{{\sum_{i=1}^{4}x}_{i}}^{2}-{4\overline{x}}^{2}}$
=$\frac{0×1+1×2+3×3+4×4.4-4×2×2.6}{{0}^{2}{+1}^{2}{+3}^{2}{+4}^{2}-4{×2}^{2}}$
=$\frac{9.8}{10}$
=0.98,
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=2.6-0.98×2=0.64;
所求的回归直线方程为$\widehat{y}$=0.98x+0.64.
点评 本题考查了散点图与求回归直线方程的应用问题,是基础题.

练习册系列答案
相关题目
9.已知0<α<$\frac{π}{2}$,若m=lg$\sqrt{1+cosα}$,n=lg$\frac{1}{\sqrt{1-cosα}}$,则sinα等于( )
| A. | 10m+n | B. | 10m-n | C. | 10mn | D. | 10${\;}^{\frac{m}{n}}$ |
19.已知a>0,函数f(x)=ax2+bx+c,若x0满足2ax0+b=0,则下列选项中是假命题的是( )
| A. | ?x∈R,f(x)≤f(x0) | B. | ?x∈R,f(x)≥f(x0) | C. | ?x∈R,f(x)≤f(x0) | D. | ?x∈R,f(x)≥f(x0) |
4.函数f(x)=x2-4x+3的最小值是( )
| A. | 3 | B. | 0 | C. | -1 | D. | -2 |
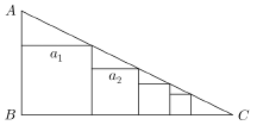 如图,在Rt△ABC内有一系列的正方形,它们的边长依次为a1,a2,…,an,…,若AB=a,BC=2a,则所有正方形的面积的和为$\frac{4}{5}{a}^{2}$.
如图,在Rt△ABC内有一系列的正方形,它们的边长依次为a1,a2,…,an,…,若AB=a,BC=2a,则所有正方形的面积的和为$\frac{4}{5}{a}^{2}$.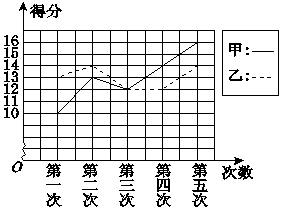 甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.
甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.