题目内容
11.△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B=$\frac{π}{3}$.分析 根据正弦定理和两角和的正弦公式和诱导公式计算即可
解答 解:∵2bcosB=acosC+ccosA,由正弦定理可得,
2cosBsinB=sinAcosC+sinCcosA=sin(A+C)=sinB,
∵sinB≠0,
∴cosB=$\frac{1}{2}$,
∵0<B<π,
∴B=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$
点评 本题考查了正弦定理和两角和的正弦公式和诱导公式,属于基础题

练习册系列答案
相关题目
1.已知a,b∈R,则“|a|+|b|>1”是“b<-1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
6.若a>1,则双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的离心率的取值范围是( )
| A. | ($\sqrt{2}$,+∞) | B. | ($\sqrt{2}$,2) | C. | (1,$\sqrt{2}$) | D. | (1,2) |
1.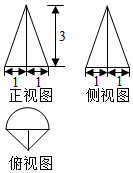 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm2)是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm2)是( )
 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm2)是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm2)是( )| A. | $\frac{π}{2}$+1 | B. | $\frac{π}{2}$+3 | C. | $\frac{3π}{2}$+1 | D. | $\frac{3π}{2}$+3 |
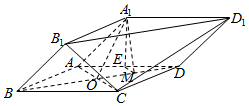 由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,
由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,