题目内容
设函数f(x)的定义域为I,现作如下定义:若?k,b∈R恒成立,使得?x∈I,f(x)≥kx+b恒成立,那么我们就称为“线托”函数.请问下列函数中是“线托”函数的是
(1)f(x)=x3
(2)f(x)=lnx-x+1
(3)f(x)=
(4)f(x)=3x-a(a∈R)
(5)f(x)=x+sinx+cosx.
(1)f(x)=x3
(2)f(x)=lnx-x+1
(3)f(x)=
| lnx |
| x |
(4)f(x)=3x-a(a∈R)
(5)f(x)=x+sinx+cosx.
考点:进行简单的合情推理
专题:推理和证明
分析:根据已知中“线托”函数的定义,分析“线托”函数图象的特点,逐一分析五个函数是否满足“线托”函数的定义,进而可得答案.
解答:
解:由已知中“线托”函数的定义可得:“线托”函数的不能为减函数,当函数为增函数时,不能为凸函数,
(1)中,f(x)=x3在x<0时为凸函数,不满足要求;
(2)中,f(x)=lnx-x+1在x>1时为减函数,不满足要求;
(3)中,f(x)=
在x>e时为减函数,不满足要求;
(4)中,f(x)=3x-a(a∈R)为增函数且为凹函数,满足要求;
(5)中,f(x)=x+sinx+cosx≥x-
恒成立,满足要求;
故答案为:(4)(5)
(1)中,f(x)=x3在x<0时为凸函数,不满足要求;
(2)中,f(x)=lnx-x+1在x>1时为减函数,不满足要求;
(3)中,f(x)=
| lnx |
| x |
(4)中,f(x)=3x-a(a∈R)为增函数且为凹函数,满足要求;
(5)中,f(x)=x+sinx+cosx≥x-
| 2 |
故答案为:(4)(5)
点评:本题考查的知识点是合情推理,其中正确理解“线托”函数的概念是解答的关键.

练习册系列答案
相关题目
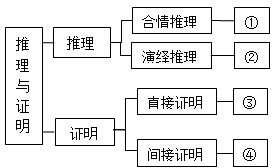 如图是选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“分析法”,则应该放在图( )
如图是选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“分析法”,则应该放在图( )| A、“①”处 | B、“②”处 |
| C、“③”处 | D、“④”处 |
执行如图所示的程序框图,当输出值为4时,输入x的值为( )


| A、2 | B、±2 |
| C、-2或-3 | D、2或-3 |
已知a>1,函数y=a|x2-x-2|的图象与函数y=|logax|的图象的交点个数是( )
| A、0 | B、1 | C、2 | D、3 |
