题目内容
(满分13分)如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,

求证: (1)FD∥平面ABC;
(1)FD∥平面ABC;
(2)AF⊥平面EDB.
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)取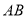 的中点
的中点 ,连接
,连接 ,利用三角形的中位线定理得出四边形
,利用三角形的中位线定理得出四边形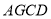 为平行四边形,再利用线面平行的判定定理进行证明;(2)利用等腰三角形的三线合一证明
为平行四边形,再利用线面平行的判定定理进行证明;(2)利用等腰三角形的三线合一证明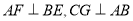 ,再利用线面垂直的判定与性质进行证明.
,再利用线面垂直的判定与性质进行证明.
解题思路: 空间中线面的平行或垂直关系的判定与证明,要注意线线关系、线面关系、面面关系的相互转化,合理结合平面几何知识进行证明.
试题解析:(1)取AB中点G,连CG,FG,由已知中F是BE的中点,结合三角形中位线的性质,可得FG平行且等于AE的一半,又由EA、CD都垂直于平面ABC,且EA=2a,DC=a,可得四边形DEGC是平行四边形,进而得到DF∥CG,由线面平行的判定定理即可得到FD∥平面ABC;
(2)由已知中EA垂直于平面ABC,则EA⊥CG,又由△ABC是正三角形,可得CG⊥AB,由线面垂直的判定定理,可得CG⊥平面EAB,进而DF⊥平面EAB,结合面面垂直的判定定理即可得到平面EAB⊥平面EDB.
证明:(1)取AB中点G,连CG,FG
四边形DEGC是平行四边形,
得到DF∥CG
DF?平面ABC,CG?平面ABC
所以FD∥平面ABC;
(2)可以证明CG⊥平面EAB,
又DF∥CG,所以DF⊥平面EAB
DF?平面EBD,所以,平面EAB⊥平面EDB
考点:1.线面平行的判定;2.线面垂直的判定与性质.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 ,所在圆的半径为10cm,则扇形的面积为___________.
,所在圆的半径为10cm,则扇形的面积为___________.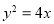 的焦点为
的焦点为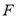 ,准线为
,准线为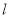 ,经过
,经过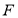 且斜率为
且斜率为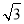 的直线与抛物线在
的直线与抛物线在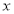 轴上方的部分相交于点
轴上方的部分相交于点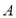 ,
,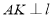 ,垂足为
,垂足为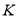 ,则
,则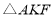 的面积是( )
的面积是( )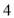 B.
B.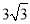 C.
C.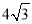 D.8
D.8 γ=m,β
γ=m,β γ=n,m∥n ,则α∥β;
γ=n,m∥n ,则α∥β; 与直线
与直线 平行,则它们之间的距离为( )
平行,则它们之间的距离为( ) B.
B. C.
C. D.
D.
 ,函数
,函数 在区间
在区间 上是( )
上是( ) B.增函数且
B.增函数且
 D.减函数且
D.减函数且
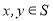 ,都有
,都有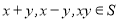 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题: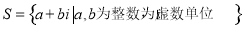 为封闭集;
为封闭集;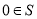 ;
;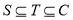 的任意集合
的任意集合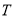 也是封闭集.
也是封闭集. 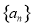 中,
中,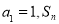 为其前
为其前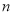 项和,且对任意
项和,且对任意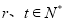 ,都有
,都有 .
.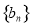 满足
满足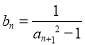 ,求数列
,求数列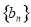 的前
的前 项和
项和 .
.