题目内容
12.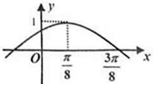 函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.
函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.
分析 根据图象求出A,ω 和φ,即可求函数f(x)的解析式;从而在求f(x)的单调递减区间.
解答 解:解:(1)由题设图象知,A=1,周期T=4($\frac{3π}{8}-\frac{π}{8}$)=π,
∴ω=$\frac{2π}{T}$=2.
∵点($\frac{π}{8}$,1)在函数图象上,
∴sin(2×$\frac{π}{8}$+φ)=1,即$\frac{π}{4}$+φ=$\frac{π}{2}+2kπ$,k∈Z.
又∵0<φ<$\frac{π}{2}$,
∴φ=$\frac{π}{4}$.
得函数f(x)的解析式为:f(x)=sin(2x+$\frac{π}{4}$).
由$\frac{π}{2}+2kπ≤2x+\frac{π}{4}≤\frac{3π}{2}+2kπ$,k∈Z.
的:$\frac{π}{4}+kπ$≤x≤$\frac{5π}{8}+kπ$.
函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.
故答案为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.
点评 本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.

练习册系列答案
相关题目
3.已知命题p:直线l1:2ax+y+1=0,l2:x+2ay+2=0,l1∥l2的充分不必要条件是a=$\frac{1}{2}$;命题q:?x∈(0,π),sinx+$\frac{1}{sinx}$>2,则下列判断正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
4.已知F为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点,A是椭圆的短轴的上顶点,点B在x轴上,且AF⊥AB,A,B,F三点确定的圆C恰好与直线x+my+3=0相切,则m的值为( )
| A. | ±3 | B. | $\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | 3 |
15.将A,B,C,D,E排成一列,要求A,B,C在排列中顺序为“A,B,C”或“C,B,A”( A,B,C可以不相邻),这样的排列数有( )
| A. | 12种 | B. | 20种 | C. | 40种 | D. | 60种 |
16.设集合A={x|2x2-5x-3≤0},B={y|y=log2(x2+3x-4)},则A∩B=( )
| A. | [-3,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,3] | C. | (1,3] | D. | (4,+∞) |