题目内容
16.设集合A={x|2x2-5x-3≤0},B={y|y=log2(x2+3x-4)},则A∩B=( )| A. | [-3,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,3] | C. | (1,3] | D. | (4,+∞) |
分析 解关于A、B的不等式,求出A、B的范围,取交集即可.
解答 解:由2x2-5x-3≤0,得-$\frac{1}{2}$≤x≤3,∴A=[-$\frac{1}{2}$,3];
∵函数y=log2(x2+3x-4的值域为R,∴B=R,
∴A∩B=[-$\frac{1}{2}$,3],
故选:B.
点评 本题考查了集合的运算,考查解不等式问题,是一道基础题.

练习册系列答案
相关题目
4.设集合A={x|x2-x-6≤0},$B=\{x|\sqrt{x^2}>2\}$,则A∩B=( )
| A. | (2,3] | B. | (2,3) | C. | (-2,3] | D. | (-2,3) |
11.已知平面向量$\overrightarrow a=(-2,1)$,$\overrightarrow b=(1,2)$,则$|{\overrightarrow a-2\overrightarrow b}|$的值是( )
| A. | 1 | B. | 5 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
1.已知F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,设双曲线的离心率为e.若在双曲线的右支上存在点M,满足|MF2|=|F1F2|,且esin∠MF1F2=1,则该双曲线的离心率e等于( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\sqrt{5}$ | D. | $\frac{5}{2}$ |
6.已知三棱锥A-BCD的四个顶点A,B,C,D都在球O的表面上,BC⊥CD,AC⊥平面BCD,且AC=2$\sqrt{2}$,BC=CD=2,则球O的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 2$\sqrt{2}$π |
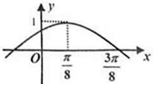 函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.
函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.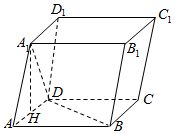 四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AD=AA1=A1D=2,H为AD中点,且A1H⊥BD.
四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AD=AA1=A1D=2,H为AD中点,且A1H⊥BD.