题目内容
4.已知F为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点,A是椭圆的短轴的上顶点,点B在x轴上,且AF⊥AB,A,B,F三点确定的圆C恰好与直线x+my+3=0相切,则m的值为( )| A. | ±3 | B. | $\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | 3 |
分析 求得椭圆的焦点坐标,设B,则圆心C($\frac{x-1}{2}$,0),半径为r=$\frac{x+1}{2}$,利用勾股定理求得x的值,利用点到直线的距离公式,即可求得m的值.
解答  解:由题意可知:椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点(-1,0),设B(x,0),
解:由题意可知:椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点(-1,0),设B(x,0),
由AF⊥AB,且A,B,F三点确定的圆C,圆心C($\frac{x-1}{2}$,0),半径为r=$\frac{x+1}{2}$,
在△AOC中,由丨AO丨2+丨OC丨2=丨AC丨2=r2,即($\sqrt{3}$)2+($\frac{x-1}{2}$)2=($\frac{x+1}{2}$)2,
解得:x=3,
则C(1,0),半径为2,
由题意可知:圆心到直线x+my+3=0距离d=$\frac{丨1+m×0+3丨}{\sqrt{1+{m}^{2}}}$=2,解得:m=±$\sqrt{3}$,
故选:C.
点评 本题考查椭圆的标准方程及简单几何性质,考查点到直线的距离公式,考查计算能力,属于中档题.

练习册系列答案
相关题目
19.已知数列{an}满足a1=1,an+1an+Sn=5,则a2=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
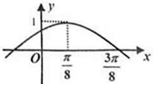 函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.
函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.