题目内容
6.自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:| 产假安排(单位:周) | 14 | 15 | 16 | 17 | 18 |
| 有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.
①求两种安排方案休假周数和不低于32周的概率;
②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望.
分析 (1)由表中信息可知,利用等可能事件概率计算公式能求出当产假为14周时某家庭有生育意愿的概率和当产假为16周时某家庭有生育意愿的概率.
(2)①设“两种安排方案休假周数和不低于32周”为事件A,由已知从5种不同安排方案中,随机地抽取2种方案选法共有10种,由此利用列举法能求出其和不低于32周的概率.
②由题知随机变量ξ的可能取值为29,30,31,32,33,34,35.分别求出相应的概率,由此能求出ξ的分布列和E(ξ).
解答 解:(1)由表中信息可知,当产假为14周时某家庭有生育意愿的概率为${P_1}=\frac{4}{200}=\frac{1}{50}$;
当产假为16周时某家庭有生育意愿的概率为${P_2}=\frac{16}{200}=\frac{2}{25}$…(2分)
(2)①设“两种安排方案休假周数和不低于32周”为事件A,
由已知从5种不同安排方案中,随机地抽取2种方案选 法共有$C_5^2=10$(种),
其和不低于32周的选法有(14、18)、(15、17)、(15、18)、(16、17)、(16、18)、(17、18),共6种,
由古典概型概率计算公式得$P(A)=\frac{6}{10}=\frac{3}{5}$…(6分)
②由题知随机变量ξ的可能取值为29,30,31,32,33,34,35.
$P(ξ=29)=\frac{1}{10}=0.1$,$P(ξ=30)=\frac{1}{10}=0.1,P(ξ=31)=\frac{2}{10}=0.2$,
$P(ξ=32)=\frac{2}{10}=0.2,P(ξ=33)=\frac{2}{10}=0.2,P(ξ=34)=\frac{1}{10}=0.1,P(ξ=35)=\frac{1}{10}=0.1$,
因而ξ的分布列为
| ξ | 29 | 30 | 31 | 32 | 33 | 34 | 35 |
| P | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 | 0.1 | 0.1 |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案| A. | (1,$\sqrt{5}$) | B. | (1,$\sqrt{5}$)∪($\sqrt{13}$,5) | C. | ($\sqrt{5}$,$\sqrt{13}$) | D. | ($\sqrt{13}$,5) |

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
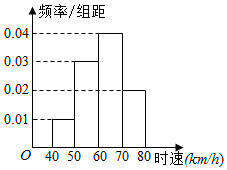 关于统计数据的分析,有以下几个结论:
关于统计数据的分析,有以下几个结论: