题目内容
如图所示,阴影部分由曲线y=
与y轴及直线y=2围成,则阴影部分的面积S= .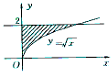
| x |

考点:定积分在求面积中的应用
专题:计算题
分析:联立
可得(4,2),进而可得S=
(2-
)dx,计算可得.
|
| ∫ | 4 0 |
| x |
解答:
解:联立
可解得
,即图中交点坐标为(4,2),
∴阴影部分的面积S=
(2-
)dx=(2x-
x
)
=
故答案为:
|
|
∴阴影部分的面积S=
| ∫ | 4 0 |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| | | 4 0 |
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:本题考查定积分求图形的面积,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
三条两两平行的直线可以确定平面的个数为( )
| A、0 | B、1 | C、0或1 | D、1或3 |
不等式(1+x2)(-2x+3)>0的解集是( )
A、{
| ||
B、{x|x<
| ||
C、{x|x>
| ||
D、{x|x>-
|
将函数y=sin(x+
)的图象上各点的横坐标伸长到原来2的倍,再向左平移
个单位,所得图象的函数解析式是( )
| π |
| 4 |
| π |
| 2 |
A、y=-sin(2x+
| ||||
B、y=sin(2x+
| ||||
C、y=cos
| ||||
D、y=sin(
|
 已知椭圆C:
已知椭圆C: