题目内容
(本题满分10分)
如图,在四边形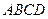 中,
中,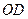 垂直平分
垂直平分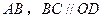 ,且
,且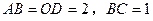 ,现将四边形
,现将四边形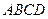 沿
沿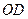 折成直二面角,求:
折成直二面角,求:
(1)求二面角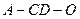 的正弦值;
的正弦值;
(2)求三棱锥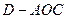 的体积.
的体积.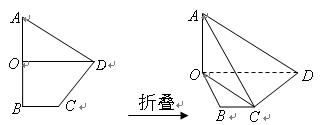
如图,在四边形
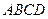 中,
中,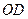 垂直平分
垂直平分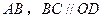 ,且
,且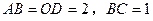 ,现将四边形
,现将四边形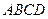 沿
沿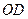 折成直二面角,求:
折成直二面角,求:(1)求二面角
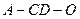 的正弦值;
的正弦值;(2)求三棱锥
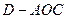 的体积.
的体积.
(1) (2)
(2)
 (2)
(2)
(1)解:因为平面 又
又
 .
. ①,
①, 又可求
又可求 又
又 ②
②
所以由①②得
 就是二面角
就是二面角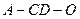 的平面角.
的平面角.
在 即所求.
即所求.
(2)
 又
又
 .
. ①,
①, 又可求
又可求 又
又 ②
②所以由①②得

 就是二面角
就是二面角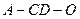 的平面角.
的平面角.在
 即所求.
即所求.(2)


练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 平面PAD;
平面PAD;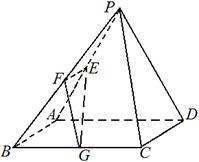
 中,
中,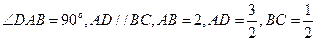
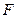 以
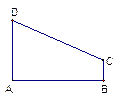
以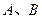 为焦点且过点
为焦点且过点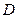 ,
,
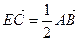 是否存在斜率
是否存在斜率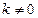 的直线
的直线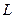 与椭圆
与椭圆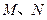 两点,且
两点,且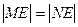 ,若存在,求
,若存在,求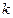 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。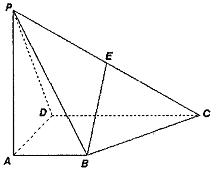
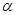 的斜线
的斜线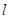 与平面
与平面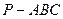 中,
中,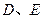 分别是
分别是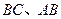 的中点,
的中点,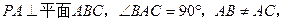
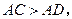
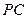 与
与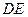 所成的角为
所成的角为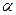 ,
,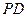 与平面
与平面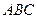 所成的角为
所成的角为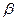 ,二面角
,二面角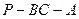 的平面角为
的平面角为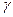 ,则
,则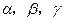 的大小关系是 ( )
的大小关系是 ( ) 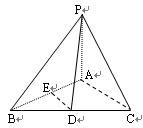
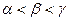
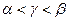
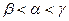
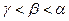
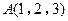 ,
,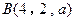 ,且
,且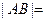
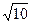 ,则
,则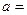 ( )
( )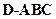 的外接球的球心O满足
的外接球的球心O满足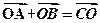 ,且外接球的体积为
,且外接球的体积为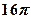 ,则该三棱锥的体积为 .
,则该三棱锥的体积为 .