题目内容
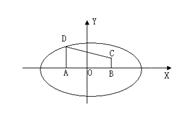
如图,直角梯形 中,
中,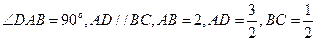
椭圆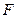 以
以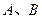 为焦点且过点
为焦点且过点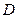 ,
,
(1)建立适当的直角坐标系,求椭圆的方程;
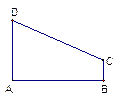
(2)若点E满足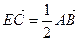 是否存在斜率
是否存在斜率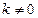 的直线
的直线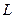 与椭圆
与椭圆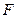 交于
交于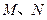 两点,且
两点,且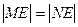 ,若存在,求
,若存在,求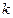 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
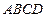 中,
中,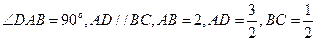
椭圆
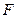 以
以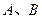 为焦点且过点
为焦点且过点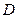 ,
,
(1)建立适当的直角坐标系,求椭圆的方程;
(2)若点E满足
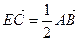 是否存在斜率
是否存在斜率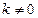 的直线
的直线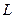 与椭圆
与椭圆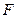 交于
交于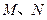 两点,且
两点,且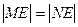 ,若存在,求
,若存在,求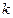 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。(1)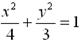 (2)
(2)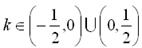
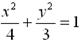 (2)
(2)
(1)以AB所在直线为x轴,AB中点为坐标原点建立直角坐标系
在RT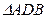 中,
中,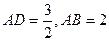
∴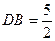
设椭圆F的方程为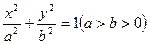
∴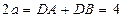 ∴
∴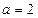
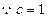 ∴
∴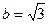
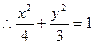 3分
3分
(2) 由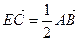 得
得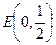
当直线L斜率不存在时,不满足 设L的方程为
代入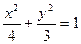 得
得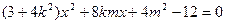
则L与椭圆有两个不同公共点的充要条件为
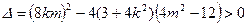 5分
5分
即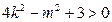
设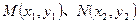 ,MN的中点为
,MN的中点为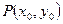
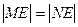 等价于
等价于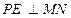
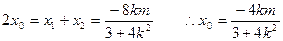 6分
6分
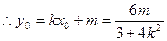 7分
7分
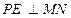 得
得  得
得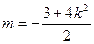 8分
8分
代入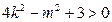 得
得 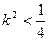 9分
9分
 10分
10分
或者用点差法
在RT
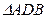 中,
中,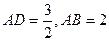
∴
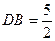
设椭圆F的方程为
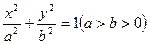
∴
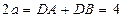 ∴
∴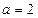
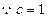 ∴
∴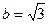
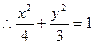 3分
3分
(2) 由
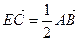 得
得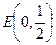
当直线L斜率不存在时,不满足 设L的方程为

代入
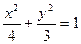 得
得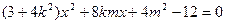
则L与椭圆有两个不同公共点的充要条件为
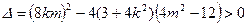 5分
5分即
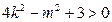
设
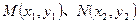 ,MN的中点为
,MN的中点为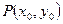
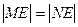 等价于
等价于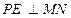
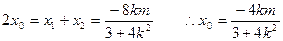 6分
6分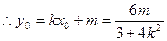 7分
7分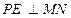 得
得  得
得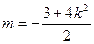 8分
8分代入
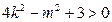 得
得 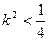 9分
9分 10分
10分或者用点差法

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;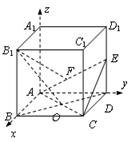
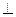 BC,AC=BC=4,四边形ABDE是直角梯形,BD
BC,AC=BC=4,四边形ABDE是直角梯形,BD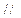 AE,BD
AE,BD
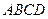 中,
中,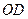 垂直平分
垂直平分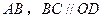 ,且
,且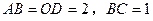 ,现将四边形
,现将四边形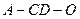 的正弦值;
的正弦值; 的体积.
的体积.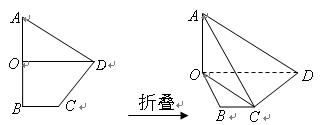
 中,底面
中,底面 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,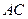 与
与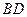 的交点为O.
的交点为O. 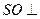 平面
平面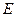 为侧棱
为侧棱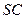 上一个动点. 试问对于
上一个动点. 试问对于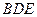 与平面
与平面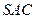 是否垂直?若垂直,请加以证明;若不垂直,请
是否垂直?若垂直,请加以证明;若不垂直,请 说明理由.
说明理由.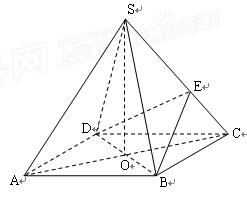
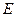 为正方体
为正方体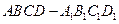 的棱
的棱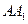 的中点,
的中点,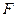 为棱
为棱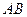 上一点,
上一点,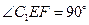 ,则
,则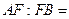 ( )
( )
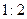
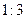
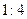
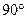 ,则称这对异面直线为“理想异面直线对”,在连结正方体各顶点的所有直线中,“理想异面直线对”的对数为
,则称这对异面直线为“理想异面直线对”,在连结正方体各顶点的所有直线中,“理想异面直线对”的对数为