题目内容
2.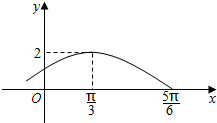 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.(1)求函数y=f(x)的解析式;
(2)当x∈[-$\frac{π}{2}$,$\frac{π}{2}$]时,求f(x)的取值范围.
分析 (1)由图象知,A,周期T,利用周期公式可求ω,由点($\frac{π}{3}$,2)在函数图象上,结合范围-$\frac{π}{2}$<φ<$\frac{π}{2}$,可求φ,从而解得函数解析式.
(2)由x∈[-$\frac{π}{2}$,$\frac{π}{2}$],可求x+$\frac{π}{6}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],利用正弦函数的图象和性质即可求得f(x)的取值范围.
解答 解:(1)由图象知,A=2,…(2分)
又$\frac{T}{4}$=$\frac{5π}{6}-$$\frac{π}{3}$=$\frac{π}{2}$,ω>0,
所以T=2π=$\frac{2π}{ω}$,得ω=1.…(4分)
所以f(x)=2sin(x+φ),
将点($\frac{π}{3}$,2)代入,得$\frac{π}{3}$+φ=2k$π+\frac{π}{2}$(k∈Z),
即φ=$\frac{π}{6}$+2kπ(k∈Z),又-$\frac{π}{2}$<φ<$\frac{π}{2}$,
所以,φ=$\frac{π}{6}$.…(6分)
所以f(x)=2sin(x+$\frac{π}{6}$).…(8分)
(2)当x∈[-$\frac{π}{2}$,$\frac{π}{2}$]时,x+$\frac{π}{6}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],…(10分)
所以sin(x+$\frac{π}{6}$)∈[-$\frac{\sqrt{3}}{2}$,1],
即f(x)∈[-$\sqrt{3}$,2].…(14分)
点评 本题是中档题,主要考查了函数的图象求出函数的解析式的方法,考查了正弦函数的图象和性质,注意视图用图能力的培养.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案| A. | 4 | B. | 6 | C. | 16 | D. | 26 |
| A. | 6 | B. | 12 | C. | 24 | D. | 60 |
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
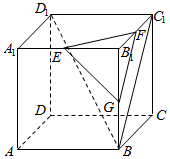 在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:①FG∥平面AA1D1D; ②EF∥平面BC1D1;
③FG∥平面BC1D1; ④平面EFG∥平面BC1D1
其中推断正确的序号是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |