题目内容
已知x,y均为正数,且x≠y,则下列四个数中最大的一个是
- A.
 (
( +
+ )
) - B.

- C.

- D.

A
分析:先取特殊的x、y值,分别代入计算,得最大的数是 ,接下来再用基本不等式和作差比较的方法,逐个加以比较大小,可以证出四个数中最大是
,接下来再用基本不等式和作差比较的方法,逐个加以比较大小,可以证出四个数中最大是 .
.
解答:先取x=1,y=2,得 =
= ,
, ,
, =
= ,
, =
=
可得最大的数是 ,接下来加以证明
,接下来加以证明
∵x,y均为正数,且x≠y,
∴x+y>2 ,可得
,可得

∵x2+y2>2xy,得2(x2+y2)>4xy
∴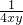 >
> >0,开方得
>0,开方得
因此, >
>
∵ -
- =
= >0
>0
∴ >
> ,
,
综上所述,四个数中最大的一个是
故选A
点评:本题给出互不相等的正数x、y,叫我们比较关于x、y的四个式子的大小关系,考查了基本不等式和作差法比较大小的知识,属于基础题.
分析:先取特殊的x、y值,分别代入计算,得最大的数是
 ,接下来再用基本不等式和作差比较的方法,逐个加以比较大小,可以证出四个数中最大是
,接下来再用基本不等式和作差比较的方法,逐个加以比较大小,可以证出四个数中最大是 .
.解答:先取x=1,y=2,得
 =
= ,
, ,
, =
= ,
, =
=
可得最大的数是
 ,接下来加以证明
,接下来加以证明∵x,y均为正数,且x≠y,
∴x+y>2
 ,可得
,可得

∵x2+y2>2xy,得2(x2+y2)>4xy
∴
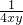 >
> >0,开方得
>0,开方得
因此,
 >
>
∵
 -
- =
= >0
>0∴
 >
> ,
,综上所述,四个数中最大的一个是

故选A
点评:本题给出互不相等的正数x、y,叫我们比较关于x、y的四个式子的大小关系,考查了基本不等式和作差法比较大小的知识,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目