题目内容
14．已知点（1，1）和（0，1）在直线3x-2y+a=0的异侧，则a的取值范围为（-1，2）．分析 由已知点（1，1）和（0，1）在直线3x-2y+a=0的异侧，我们将两点坐标代入直线方程所得符号相反，则我们可以构造一个关于a的不等式，解不等式即可得到答案
解答 解：若点（1，1）和（0，1）在直线3x-2y+a=0的异侧，
则（3-2+a）•（-2+a）＜0
即（a+1）（a-2）＜0
解得a∈（-1，2），
故答案为：（-1，2）．
点评 本题考查的知识点是二元一次不等式与平面区域，根据A、B在直线两侧，则A、B坐标代入直线方程所得符号相反构造不等式是解答本题的关键．
练习册系列答案
互动英语系列答案
相关题目
15．若向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，$\overrightarrow{a}$在$\overrightarrow{a}$+$\overrightarrow{b}$上的投影等于（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | $\sqrt{3}$ | D． | 4+2$\sqrt{3}$ |
5．下列说法正确的是（ ）
| A． | 图象连续的函数f（x）在区间（a，b）上一定存在最值 | |
| B． | 函数的极小值可能大于极大值 | |
| C． | 函数的最小值一定是极小值 | |
| D． | 函数的极小值一定是最小值 |
19．为支援西部教育事业，从某校118名教师中随机抽取16名教师组成暑期西部讲师团．若先用简单随机抽样从118名教师中剔除6名，剩下的112名再按系统抽样的方法进行，则每人入选的可能性（ ）
| A． | 不全相等 | B． | 都相等，且为$\frac{8}{59}$ | C． | 均不相等 | D． | 都相等，且为$\frac{1}{7}$ |
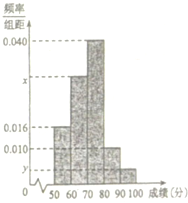某中学举行了一次“环保知识竞赛”活动，为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出如图所示的频率分布直方图，但由于不慎丢失了部分数据．已知得分在[50，60）的有8人，在[90，100）的有2人，由此推测频率分布直方图中的x=（ ）