题目内容
已知函数f(x)=loga
.求:
(1)f(x)的定义域;
(2)判断f(x)在其定义域上的奇偶性,并予以证明,
(3)求f(x)>0的解集.
| 2-x |
| 2+x |
(1)f(x)的定义域;
(2)判断f(x)在其定义域上的奇偶性,并予以证明,
(3)求f(x)>0的解集.
考点:函数的定义域及其求法,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)由对数函数的定义求出函数f(x)的定义域,(2)根据函数的奇偶性的定义进行判断即可;(3)分别讨论a>1,0<a<1时的情况,再解不等式.
解答:
解:(1)∵
>0,解得:-2<x<2,
∴f(x)的定义域为(-2,2)
(2)f(x)为定义域上的奇函数,
∵f(x)的定义域为(-2,2),关于原点对称.
f(-x)+f(x)=loga
+loga
=loga
•
=loga1=0,
∴f(x)在(-2,2)上为奇函数.
(3)a>1时,f(x)>0,
则
>1⇒-2<x<0,
f(x)>0的解集为(-2,0)
0<a<1时,f(x)>0,
则0<
<1⇒0<x<2,
f(x)>0的解集为(0,2).
∴a>1时,f(x)>0的解集为(-2,0)
0<a<1时,f(x)>0的解集为(0,2).
| 2-x |
| 2+x |
∴f(x)的定义域为(-2,2)
(2)f(x)为定义域上的奇函数,
∵f(x)的定义域为(-2,2),关于原点对称.
f(-x)+f(x)=loga
| 2+x |
| 2-x |
| 2-x |
| 2+x |
| 2+x |
| 2-x |
| 2-x |
| 2+x |
∴f(x)在(-2,2)上为奇函数.
(3)a>1时,f(x)>0,
则
| 2-x |
| 2+x |
f(x)>0的解集为(-2,0)
0<a<1时,f(x)>0,
则0<
| 2-x |
| 2+x |
f(x)>0的解集为(0,2).
∴a>1时,f(x)>0的解集为(-2,0)
0<a<1时,f(x)>0的解集为(0,2).
点评:本题考查了函数的定义域问题,对数函数的定义,函数的奇偶性,考查分类讨论,是一道中档题.

练习册系列答案
相关题目
有一段“三段论”推理是这样的:对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点,因为函数f(x)=x3在x=0处的导数值f′(x0)=0,所以,x=0是函数f(x)=x3的极值点.以上推理中( )
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、结论正确 |
下列命题中,正确的命题的个数是( )
a.若角α在第二象限,且sinα=m,cosα=n,则tanα=-
b.无论α为何角,都有sin2α+cos2α=1
c.总存在一个角α,使得sinα+cosα=1
d.总存在一个角α,使得sinα=cosα=
.
a.若角α在第二象限,且sinα=m,cosα=n,则tanα=-
| m |
| n |
b.无论α为何角,都有sin2α+cos2α=1
c.总存在一个角α,使得sinα+cosα=1
d.总存在一个角α,使得sinα=cosα=
| 1 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
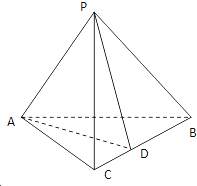 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC,点D为BC中点.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC,点D为BC中点.