题目内容
在四面体ABCD中,AB⊥面BCD,BC=CD,∠BCD=90°,∠ADB=30°,E,F分别是AC,AD的中点,分别求出面BEF与面ABC的法向量,并据此说明平面BEF与平面ABC的位置关系.
考点:平面与平面之间的位置关系
专题:空间向量及应用
分析:首先,设出A(0,0,a),然后,得到D(0,
a,0),B(0,0,0),C(
a,
a,0),E(
a,
a,
a),F(0,
a,
a),从而得到
=(
a,
a,0),
=(0,0,a),
=(
a,
a,
a),
=(0,
a,
a),最后,结合法向量进行求解.
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| BC |
| ||
| 2 |
| ||
| 2 |
| BA |
| BE |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| BF |
| ||
| 2 |
| 1 |
| 2 |
解答:
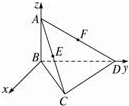 解:由设A(0,0,a)及∠ADB=30°,得
解:由设A(0,0,a)及∠ADB=30°,得
点D(0,
a,0),B(0,0,0)
又BC=CD,∠BCD=90°,得
C(
a,
a,0),
由E、F分别是AC、AD的中点,得
E(
a,
a,
a),F(0,
a,
a),
∴
=(
a,
a,0),
=(0,0,a),
=(
a,
a,
a),
=(0,
a,
a),
设平面BEF的法向量为
=(α,β,γ),
∴
,
∴
,
∴取
,
∴
=(0,1,-
),
设平面ABC的法向量为
=(x,y,z),
∴
,
∴
,
∴取
,
∴
=(1,-1,0),
∵
•
=-1≠0,
∴平面BEF与平面ABC相交.
 解:由设A(0,0,a)及∠ADB=30°,得
解:由设A(0,0,a)及∠ADB=30°,得点D(0,
| 3 |
又BC=CD,∠BCD=90°,得
C(
| ||
| 2 |
| ||
| 2 |
由E、F分别是AC、AD的中点,得
E(
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴
| BC |
| ||
| 2 |
| ||
| 2 |
| BA |
| BE |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| BF |
| ||
| 2 |
| 1 |
| 2 |
设平面BEF的法向量为
| μ1 |
∴
|
∴
|
∴取
|
∴
| μ1 |
| 3 |
设平面ABC的法向量为
| μ2 |
∴
|
∴
|
∴取
|
∴
| μ2 |
∵
| μ1 |
| μ2 |
∴平面BEF与平面ABC相交.
点评:本题重点考查了空间向量的运算、平面的法向量等知识,属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
根据如下样本数据:
得到的回归方程为
=
x+
,则( )
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 | -3 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
关于平面向量
、
、
,有下列四种说法:
①若
≠0,
•
=0,则
=0;
②若
≠0,
•
=
•
,则
=
;
③对任意向量
、
、
,有(
•
)•
=
•(
•
);
④若
∥
,
∥
,则
∥
,
其中正确的个数是( )
| a |
| b |
| c |
①若
| a |
| a |
| b |
| b |
②若
| a |
| a |
| b |
| a |
| c |
| b |
| c |
③对任意向量
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
④若
| a |
| b |
| b |
| c |
| a |
| c |
其中正确的个数是( )
| A、0 | B、1 | C、2 | D、3 |
函数y=3x-8+log2x的零点一定位于的区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
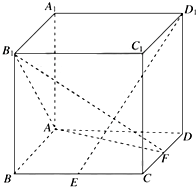 如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,点F是棱CD上的动点.
如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,点F是棱CD上的动点.