题目内容
7.已知椭圆:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,上顶点为B,右焦点为F,过A、B、F作圆C,若圆心C的横纵坐标相等,则该椭圆的离心率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由题意可得A(-a,0),B(0,b),F(c,0),即有圆心C在AF的中垂线上,可得xC=$\frac{c-a}{2}$,再由圆的定义可得|CA|=|CB|,运用两点的距离公式和离心率公式,计算即可得到所求值.
解答 解:由题意可得A(-a,0),B(0,b),F(c,0),
即有圆心C在AF的中垂线上,可得xC=$\frac{c-a}{2}$,
由题意可得圆心C($\frac{c-a}{2}$,$\frac{c-a}{2}$),
由|CA|=|CB|,
可得$\sqrt{(\frac{c+a}{2})^{2}+(\frac{c-a}{2})^{2}}$=$\sqrt{(\frac{c-a}{2})^{2}+(\frac{c-a-2b}{2})^{2}}$,
即有(c+a)2=(c-a-2b)2,
即(2c-2b)(2a+2b)=0,
由a>b>0,可得c=b,
由b2=a2-c2,可得c2=2a2,
e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题考查椭圆的离心率的求法,注意运用圆的定义,以及两点的距离公式,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
19.已知扇形的周长为10,扇形圆心角的弧度数是3,则扇形的面积为( )
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
17.椭圆4x2+y2=k上任意两点的最大距离为8,则k的值为( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
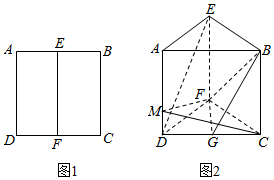 如图1,在边长为4的正方形ABCD中,E、F分别是AB、CD的中点,沿EF将矩形ADFE折起使得二面角A-EF-C的大小为90°(如图2),点G是CD的中点
如图1,在边长为4的正方形ABCD中,E、F分别是AB、CD的中点,沿EF将矩形ADFE折起使得二面角A-EF-C的大小为90°(如图2),点G是CD的中点