题目内容
(本小题满分13分)设集合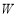 由满足下列两个条件的数列
由满足下列两个条件的数列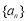 构成:
构成:
①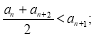 ②存在实数
②存在实数 ,使
,使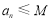 .(
.( 为正整数)
为正整数)
(Ⅰ)在只有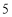 项的有限数列
项的有限数列 ,
, 中,其中
中,其中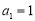 ,
,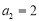 ,
,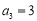 ,
,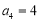 ,
, ,
,
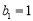 ,
,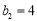 ,
, ,
, ,
, ,试判断数列
,试判断数列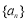 ,
, 是否为集合
是否为集合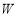 的元素;
的元素;
(Ⅱ)设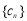 是等差数列,
是等差数列,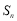 是其前
是其前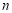 项和,
项和,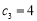 ,
, ,证明数列
,证明数列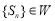 ;并求出
;并求出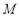 的取值范围.
的取值范围.
(2)
【解析】
试题分析:(Ⅰ)对于数列 ,当
,当 时,
时, ,显然不满足集合W的条件①,
,显然不满足集合W的条件①,
故 不是集合W中的元素,
不是集合W中的元素,
对于数列 ,当
,当 时,
时,
不仅有
而且有 ,
,
显然满足集合W的条件①②,故 是集合W中的元素.
是集合W中的元素.
(Ⅱ)∵ 是等差数列,
是等差数列, 是其前n项和,
是其前n项和,
 .设其公差为d,∴
.设其公差为d,∴ .
.
∴
∴ ,
,
∵
∵ ,∴
,∴ 的最大值是
的最大值是 ,
,
即 .
.
∴ ,且M的取值范围是
,且M的取值范围是 .
.
考点:本题考查数列综合应用

练习册系列答案
相关题目
 已知函数
已知函数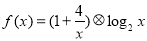 ,若函数
,若函数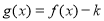 恰有两个零点,则
恰有两个零点,则 的取值范围为
的取值范围为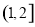 B.
B. 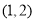 C.
C. 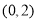 D.
D. 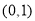
 ,
, ,则
,则 .
. 是两个非零的平面向量,则 “
是两个非零的平面向量,则 “ ”是“
”是“ ”的
”的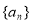 中,
中,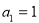 ,且
,且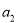 是
是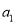 和
和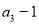 的等差中项.
的等差中项.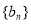 满足
满足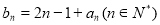 ,求
,求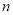 项和
项和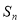 .
. ,若存在区间
,若存在区间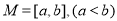 ,使得
,使得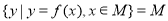 ,则称区间
,则称区间 为函数
为函数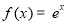 (B)
(B)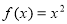 (C)
(C)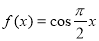 (D)
(D)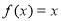
 的左焦点作倾斜角为
的左焦点作倾斜角为 的直线
的直线 ,则直线
,则直线 中,
中, ,则
,则 等于
等于 B.
B. C.
C. D.
D.