题目内容
7.已知函数$f(x)=\left\{{\begin{array}{l}{\frac{x}{x-1},x≤0}\\{-{x^2}+6x-5,x>0}\end{array}}\right.$,若函数y=f[f(x)-a]有6个零点,则实数a的取值范围是( )| A. | -4≤a≤1 | B. | -5≤a≤-4 | C. | 0≤a≤1 | D. | -5≤a≤-1 |
分析 先求出f(x)的零点,然后求出f(x)-a的值,作出函数f(x)的图象,利用数形结合以及排除法进行求解即可.
解答 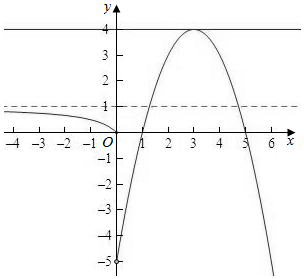 解:当x≤0时,由f(x)=0得$\frac{x}{x-1}$=0,得x=0,
解:当x≤0时,由f(x)=0得$\frac{x}{x-1}$=0,得x=0,
当x>0时,由f(x)=0得-x2+6x-5=0,得x=1或x=5,
由,y=f[f(x)-a]=0得f(x)-a=0或f(x)-a=1,或f(x)-a=5,
即f(x)=a,f(x)=a+1,f(x)=a+5,
作出函数f(x)的图象如图:
若a=0,则f(x)=0有3个根,f(x)=1有2个根,f(x)=5有0个根,此时共有5个根,不满足条件.排除A,C,
若a=-1,则f(x)=-1有2个根,f(x)=0有3个根,f(x)=4有1个根,此时共有6个根,满足条件.排除B,
故选:D.
点评 本题主要考查函数与方程的应用,求出函数的零点,利用数形结合以及分类讨论是解决本题的关键.本题由于难度较大,使用特殊值法和排除法是解决本题的技巧.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
17.在等差数列{an}中,a3-a2=-2,a7=-2,则a9=( )
| A. | 2 | B. | -2 | C. | -4 | D. | -6 |
18.已知31=3,32=9,33=27…,则32016的个位数上数字为( )
| A. | 1 | B. | 3 | C. | 7 | D. | 9 |
2.已知集合A={x|2x2-7x+3≤0,x∈R},B={x|0<x≤1}则集合A∩B=( )
| A. | $(0,\frac{1}{2}]$ | B. | [1,3] | C. | $[\frac{1}{2},1]$ | D. | (0,1] |
12.已知A={-2,-1,0,1,2},B={x|2x-1>0},则A∩B=( )
| A. | {-2,-1,0,1,2} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
17.已知在数列{an}中,a1=$\frac{4}{5}$,an+1=$\left\{\begin{array}{l}{2{a}_{n},{a}_{n}∈[0,\frac{1}{2}]}\\{2{a}_{n}-1,{a}_{n}∈(\frac{1}{2},1]}\end{array}\right.$,则a2015等于( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |