题目内容

2．已知集合A={x|2x2-7x+3≤0，x∈R}，B={x|0＜x≤1}则集合A∩B=（　　）
A．$（0，\frac{1}{2}]$B．[1，3]C．$[\frac{1}{2}，1]$D．（0，1]

分析 求出A与B中不等式的解集确定出A与B，找出两集合的交集即可．

解答 解：由A中的不等式变形得：（2x-1）（x-3）≤0，
解得：$\frac{1}{2}$≤x≤3，即A=[$\frac{1}{2}$，3]；
B=（0，1]，
∴A∩B=[$\frac{1}{2}$，1]．
故选：C．

点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案
相关题目
12．已知f（x）是定义在R上的奇函数，当x＜0时，f（x）=ex（x+1），给出以下命题：
①当x＞0时，f（x）=ex（1-x）；
②f（x）有3个零点；
③f（x）＞0的解集为（-1，0）∪（1，+∞）；
④?x1，x2∈R，都有|f（x1）-f（x2）|≤2，
其中正确命题的序号是②③④（填上所有正确命题的序号）
13．一几何体的三视图是如图所示的三个直角边为2的等腰直角三角形，则该几何体的表面积为（　　）
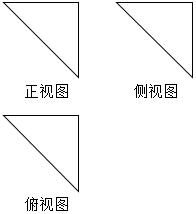
A．8B．4$\sqrt{3}$+4C．4$\sqrt{2}$+4D．6+2$\sqrt{3}$
10．已知数列{an}为等差数列，若a1，a2，a3成等比数列，且a1=1，则公差d=（　　）
A．0B．1C．2D．4
17．已知函数$f（x）=\left\{{\begin{array}{l}{x+\frac{1}{x}+a，x＞0}\\{{2^x}+a，x≤0}\end{array}}\right.$，若方程f（x）=-x有且仅有一解，则实数a的取值范围为a≥-1或a=-2$\sqrt{2}$．．
7．已知函数$f（x）=\left\{{\begin{array}{l}{\frac{x}{x-1}，x≤0}\\{-{x^2}+6x-5，x＞0}\end{array}}\right.$，若函数y=f[f（x）-a]有6个零点，则实数a的取值范围是（　　）
A．-4≤a≤1B．-5≤a≤-4C．0≤a≤1D．-5≤a≤-1
14．设a∈R，则“a＞1”是“a2＞|a-2|”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
11．判断函数的奇偶性：函数f（x）=x3•1g$\frac{1-x}{1+x}$是偶函数．
12．已知函数f（x）=$\left\{\begin{array}{l}{|lnx|，x＞0}\\{|{x}^{2}+4x+3|，x≤0}\end{array}\right.$若关于x的方程f2（x）+bf（x）+4=0有8个不同的实数根，则实数b的取值范围是（　　）
A．[-$\frac{17}{4}$，-4）∪{-5}B．[-$\frac{13}{3}$，-4）∪{-5}C．[-5，-$\frac{13}{3}$]D．[-5，-4]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网