题目内容
11.设a>0,函数f(x)=$\frac{{e}^{x}}{a}$+$\frac{a}{{e}^{x}}$是定义在R上的偶函数.(1)求函数f(x)的解析式;
(2)证明:f(x)在(0,+∞)上是增函数.
分析 (1)直接运用函数奇偶性性的定义求函数的解析式;
(2)运用函数单调性的定义和指数函数的性质证明函数的单调性.
解答 解:(1)因为f(x)为R上的偶函数,
所以,f(-x)=f(x)恒成立,
即$\frac{{e}^{x}}{a}$+$\frac{a}{{e}^{x}}$=$\frac{{e}^{-x}}{a}$+$\frac{a}{{e}^{-x}}$,
整理得,(a-$\frac{1}{a}$)•(ex-e-x)=0,
所以,a-$\frac{1}{a}$=0且a>0,解得a=1,
因此,f(x)=ex+e-x;
(2)任取x1,x2∈(0,+∞)且x1<x2,
则f(x1)-f(x2)=(${e}^{{x}_{1}}$+${e}^{-{x}_{1}}$)-(${e}^{{x}_{2}}$-${e}^{-{x}_{2}}$)
=(${e}^{{x}_{1}}$-${e}^{{x}_{2}}$)+(${e}^{-{x}_{1}}$-${e}^{-{x}_{2}}$)=(${e}^{{x}_{1}}$-${e}^{{x}_{2}}$)+$\frac{{e}^{{x}_{1}}-{e}^{{x}_{2}}}{{e}^{{x}_{1}}•{e}^{{x}_{2}}}$
=(${e}^{{x}_{1}}$-${e}^{{x}_{2}}$)•$\frac{{e}^{{x}_{1}+{x}_{2}}-1}{{e}^{{x}_{1}}•{e}^{{x}_{2}}}$,
因为x2>x1>0,所以,${e}^{{x}_{1}}$-${e}^{{x}_{2}}$<0,$\frac{{e}^{{x}_{1}+{x}_{2}}-1}{{e}^{{x}_{1}}•{e}^{{x}_{2}}}$>0,
所以,f(x1)-f(x2)<0,
即f(x)为(0,+∞)上的增函数.
点评 本题主要考查了函数解析式的求法,以及运用函数奇偶性和单调性的定义,考查了指数函数的图象和性质,属于中档题.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案| A. | ∅ | B. | {0} | C. | {(0,1)}和{(1,2)} | D. | {1} |
| A. | 抛掷骰子试验 | |
| B. | 抛硬币 | |
| C. | 计算器 | |
| D. | 正方体的六个面上分别写有1,2,2,3,4,5,抛掷该正方体 |
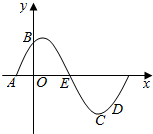 已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)一个周期内的图象上的四个点,如图所示,A(-$\frac{π}{6}$,0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,$\overrightarrow{CD}$在x轴方向上的投影为$\frac{π}{12}$.
已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)一个周期内的图象上的四个点,如图所示,A(-$\frac{π}{6}$,0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,$\overrightarrow{CD}$在x轴方向上的投影为$\frac{π}{12}$.