题目内容
3.直线x+$\sqrt{3}$y-a=0的倾斜角为( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 把直线的方程化为斜截式,求出斜率,根据斜率和倾斜角的关系,倾斜角的范围,求出倾斜角的大小.
解答 解:直线x+$\sqrt{3}$y-a=0 即 y=-$\frac{\sqrt{3}}{3}$x+a,
故直线的斜率等于-$\frac{\sqrt{3}}{3}$,设直线的倾斜角等于α,
则 0≤α<π,且tanα=-$\frac{\sqrt{3}}{3}$,
故 α=150°,
故选:D.
点评 本题考查直线的倾斜角和斜率的关系,以及倾斜角的取值范围,已知三角函数值求角的大小.求出直线的斜率是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.设f(x)是定义在R上的偶函数,f(x)在(0,3)内单调递增,且y=f(x)的图象关于直线x=3对称,则下面正确的结论是( )
| A. | f(1.5)<f(3.5)<f(6.5) | B. | f(6.5)<f(1.5)<f(3.5) | C. | f(6.5)<f(3.5)<f(1.5) | D. | f(3.5)<f(6.5)<f(1.5) |
12.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1500石,验得米内夹谷,抽样取米一把,数得250粒内夹谷30粒,则这批米内夹谷约为( )
| A. | 140石 | B. | 160石 | C. | 180石 | D. | 200石 |
13.已知一个三棱锥的三视图如图所示,若该三棱锥的四个顶点均在同一球面上,则该求的体积为( )
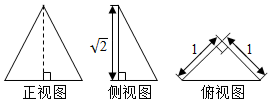

| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |