题目内容
求证:当λ变化时,直线(λ+2)x+(1-λ)y-4λ-5=0,都经过一个定点,并求该定点的坐标.
考点:恒过定点的直线
专题:直线与圆
分析:把直线(λ+2)x+(1-λ)y-4λ-5=0化为λ(x-y-4)+2x+y-5=0,利用
,求出定点P的坐标.
|
解答:
证明:∵直线(λ+2)x+(1-λ)y-4λ-5=0,
∴λ(x-y-4)+2x+y-5=0,
令
,
解得x=3,y=-1;
∴当λ变化时,该直线都经过一个定点P,
且定点P的坐标是(3,-1).
∴λ(x-y-4)+2x+y-5=0,
令
|
解得x=3,y=-1;
∴当λ变化时,该直线都经过一个定点P,
且定点P的坐标是(3,-1).
点评:本题考查了直线恒过定点的应用问题,解题时应利用分离参数的方法,是基础题目.

练习册系列答案
相关题目
数列an=
的前5项之和是( )
| 1+(-1)n |
| 2 |
| A、0 | B、2 | C、4 | D、6 |

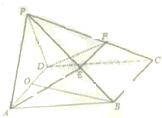 如图,已知平面PAD⊥平面ABCD,ABCD为菱形,∠BAD=60°,O是线段AD的中点,E是PB上一点,过直线AD与点E的平面与平面PBC的交线是EF.
如图,已知平面PAD⊥平面ABCD,ABCD为菱形,∠BAD=60°,O是线段AD的中点,E是PB上一点,过直线AD与点E的平面与平面PBC的交线是EF.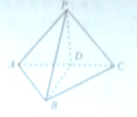 如图所示,在四面体P-ABC中,∠ABC=90°,PA=PB=PC,D是AC的中点,求证:PD垂直于△ABC所在的平面.
如图所示,在四面体P-ABC中,∠ABC=90°,PA=PB=PC,D是AC的中点,求证:PD垂直于△ABC所在的平面.