题目内容
在f(x1)=x
,f(x2)=x2,f3(x)=2x,f4(x)=log
x,四个函数中,当x1>x2>1时,使
[f(x1)+f(x2)<(
)成立的函数是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| A、f1(x) |
| B、f2(x) |
| C、f3(x) |
| D、f4(x) |
考点:函数的图象,函数单调性的性质
专题:函数的性质及应用
分析:本题考查的是函数图象的应用问题.在解答时,应先充分结合条件:“对(1,+∞)中任意的x1和x2,
[f(x1)+f(x2)<(
)成恒成立”分析函数的凸凹性,进而根据具体的变化规律作出判断.
| 1 |
| 2 |
| x1+x2 |
| 2 |
解答:
解:在同一坐标系中分别出画出f(x1)=x
(红色曲线),f(x2)=x2(绿色曲线),f3(x)=2x(蓝色曲线),f4(x)=log
x(黄色曲线)如图所示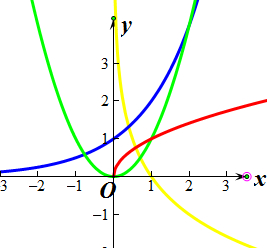
由题意可知:函数f(x)满足性质:“对(1,+∞)中任意的x1和x2,
[f(x1)+f(x2)<(
)成恒成立”.
∴函数图象在(1,+∞)上为上凸函数,
有所给图象可知:f(x2),f(x3),f(x4)均为下凸函数;故不符合题意.
从而只有A适合上凸的性质.
故选:A.
| 1 |
| 2 |
| 1 |
| 2 |

由题意可知:函数f(x)满足性质:“对(1,+∞)中任意的x1和x2,
| 1 |
| 2 |
| x1+x2 |
| 2 |
∴函数图象在(1,+∞)上为上凸函数,
有所给图象可知:f(x2),f(x3),f(x4)均为下凸函数;故不符合题意.
从而只有A适合上凸的性质.
故选:A.
点评:本题考查的是函数图象的应用问题.在解答的过程当中充分体现了隐含条件的挖掘、数形结合的思想以及问题转化的能力.值得同学们体会反思.

练习册系列答案
相关题目
已知a1=3,an+1=
,试通过计算a2,a3,a4,a5的值推测出an=( )
| 3an |
| an+3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=sin(x+
)cos(
-x)的最大值及最小正周期分别为( )
| π |
| 3 |
| π |
| 6 |
A、
| ||
B、
| ||
| C、1,π | ||
| D、1,2π |
已知角α的终边过点P(4,-3),则sinα的值是( )
A、-
| ||
B、
| ||
C、-
| ||
| D、与α的取值有关 |
函数y=sin(x+
)的图象可由y=sinx图象经过下述( )变换得到.
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向上平移
| ||
D、向下平移
|
函数y=x2-2tx+3在[1,+∞)上为增函数,则t的取值范围是( )
| A、t≤1 | B、t≥1 |
| C、t≤-1 | D、t≥-1 |
若(
+
)n的展开式中前三项的系数成等差数列,则展开式中的有理项共有( )
| x |
| 1 | |||
2
|
| A、2项 | B、3项 | C、4项 | D、5项 |