题目内容
3.已知目标函数z=2x+y且变量x,y满足下列条件$\left\{\begin{array}{l}x-4y≤-3\\ 3x+5y<25\\ x≥1\end{array}\right.$,则( )| A. | zmax=12,zmin=3 | B. | zmax=12,无最小值 | ||
| C. | 无最大值,zmin=3 | D. | 无最小值也无最大值 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x-4y≤-3\\ 3x+5y<25\\ x≥1\end{array}\right.$作出可行域如图,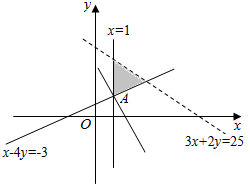
联立$\left\{\begin{array}{l}{x=1}\\{x-4y=-3}\end{array}\right.$,解得A(1,1),
化目标函数z=2x+y为y=-2x+z.
由图可知,当直线过A时,直线在y轴上的截距最小,z有最小值为3.
目标函数无最大值.
故选:C.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下面表中所示:
(1)请根据上表的数据,估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否在出错的概率不超过1%的前提下,认为该地老年人是否需要帮助与性别有关?并说明理由;
(3)根据(2)的结论,你能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?并说明理由.
附:独立性检验卡方统计量${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量,独立性检验临界值表为:
| 性别 是否需要帮助 | 男 | 女 | 合计 |
| 需要 | 50 | 25 | 75 |
| 不需要 | 200 | 225 | 425 |
| 合计 | 250 | 250 | 500 |
(2)能否在出错的概率不超过1%的前提下,认为该地老年人是否需要帮助与性别有关?并说明理由;
(3)根据(2)的结论,你能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?并说明理由.
附:独立性检验卡方统计量${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量,独立性检验临界值表为:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
8.已知函数f(x)=x+ex,g(x)=x+lnx,h(x)=lnx-1的零点依次为a,b,c,则a,b,c从大到小的顺序为( )
| A. | c>b>a | B. | c>a>b | C. | b>c>a | D. | a>c>b |
13.已知$sin\frac{α}{2}-cos\frac{α}{2}=-\frac{{\sqrt{2}}}{2}$,且cosα<0,则tanα=( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |