题目内容
20.某三棱锥的三视图是三个边长相等的正方形及对角线,若该三棱锥的体积是$\frac{1}{3}$,则它的表面积是2$\sqrt{3}$.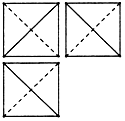
分析 根据三视图得出该几何体是正方体的内接正三棱锥,画出图形求出三棱锥的棱长,
利用面积公式求出几何体的表面积.
解答 解:如图所示,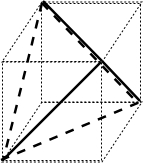
该几何体是正方体的内接正三棱锥;
设正方体的棱长为a,
则几何体的体积是
V=a3-4×$\frac{1}{3}$×$\frac{1}{2}$a2•a=$\frac{1}{3}$a3=$\frac{1}{3}$,
∴a=1,
∴三棱锥的棱长为$\sqrt{2}$,
因此该三棱锥的表面积为
S=4×$\frac{\sqrt{3}}{4}$×${(\sqrt{2})}^{2}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了正方体的内接正三棱锥表面积的计算问题,关键是根据三视图得出几何体的结构特征.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
10.圆E经过三点A(0,1),B(2,0),C(0,-1),且圆心在x轴的正半轴上,则圆E的标准方程为( )
| A. | (x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$ | B. | (x+$\frac{3}{4}$)2+y2=$\frac{25}{16}$ | C. | (x-$\frac{3}{4}$)2+y2=$\frac{25}{16}$ | D. | (x-$\frac{3}{4}$)2+y2=$\frac{25}{4}$ |
15.在△ABC中,$AB=3,AC=2,\overrightarrow{BD}=\frac{1}{2}\overrightarrow{BC},则\overrightarrow{AD}•\overrightarrow{DB}$的值为( )
| A. | $\frac{5}{2}$ | B. | $-\frac{5}{2}$ | C. | $\frac{5}{4}$ | D. | $-\frac{5}{4}$ |
9.某三棱锥的三视图如图所示,该三棱锥的体积是( )
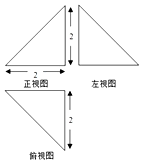

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $6+2\sqrt{3}$ |
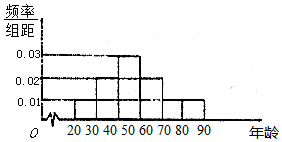 退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势,某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示,若规定年龄分布在60~80岁(含60岁和80岁)为“老年人”.
退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势,某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示,若规定年龄分布在60~80岁(含60岁和80岁)为“老年人”.